1. Introduction

Nous traitons dans cet article d’un travail de résolution d’un problème numérique, le problème dit du géant (Figure 1), par des élèves de 10 - 11 ans, et des modalités d’enseignement mises en place pour étayer ce travail dans le cadre d’une ingénierie didactique. La partie expérimentale de cette ingénierie a été menée en 2008 par le groupe ACODIS IUFM-UDS ¹ (Adjiage & Rauscher, 2013). Elle repose sur l’observation d’une séquence de classe de six séances (Tableau I en annexe).

La résolution du problème du géant nécessite un processus de modélisation, c’est-à-dire, pour être bref, la substitution à l’univers représenté d’un univers représentant parce que « le problème posé dans l’univers représenté n’y est pas résoluble. » (Brousseau, 2003, p. 13). Pour un « expert » s’appuyant sur ses connaissances théoriques et empiriques ce problème n’est pas vraiment un problème de recherche. En revanche, pour des élèves de 10-11 ans ne possédant pas un référentiel de connaissances bien établi, il devient le terrain d’une pensée mathématique de recherche comme la décrivent Bkouche, Charlot et Rouche (1991) : « Résoudre un problème n’est pas une activité principalement déductive. L’esprit s’anime dans le désordre apparent de la pensée créatrice. Il fait des conjectures, cherche des exemples et des contre-exemples, amorce des raisonnements, remonte l’ordre déductif par l’opération d’analyse, renforce ou allège les hypothèses, etc. » (p.144). Notre ingénierie nous a donné l’occasion de recueillir de nombreuses productions écrites des élèves. Celles-ci témoignent de ce travail de la pensée mathématique des élèves confrontés à ce problème bien particulier de modélisation. Nous utilisons ici le cadre ETM proposé par Alain Kuzniak (2011) comme une coquille méthodologique qui nous permettra dans un premier temps :

• d’analyser le travail d’un expert résolvant ce problème dans un ETM de référence,

• d’analyser la diversité des pensées mathématiques initiales des élèves abordant ce problème dans leurs ETM personnels.

Dans un deuxième temps, nous aurons l’occasion de revisiter notre ingénierie pour repérer :

• l’occasion perdue d’aménager un ETM idoine à partir des ETM personnels pour permettre aux élèves de développer des solutions efficaces à partir de leurs procédures initiales,

• l’efficacité de l’ETM idoine que nous avions réellement en nous appuyant sur une pratique « écrite de l’écrit » (Duval, 2001, p.197). C’est dans cet espace idoine que bon nombre d’élèves ont pu finalement résoudre le problème en intégrant les modalités d’un processus de modélisation.

2. Le problème du géant et sa résolution

Enoncé : Cette photo a été prise dans un parc d’attraction en Angleterre. On y aperçoit une partie de la jambe d’un géant. Quelle est la taille de ce géant ?

Le problème du géant est un problème de Fermi ³ et répond au cahier de charge proposé par Peter - Koop (2004) dans ce cadre.

• Aucun nombre n’est fourni dans l’énoncé

• Résoudre ce problème nécessite de faire des hypothèses : taille d’un des hommes de la photo, proportions du géant, taille d’un pied d’homme...

• La réponse dépend des hypothèses et de la précision des mesures adoptées et des mesurages (stature d’un homme, semelle du géant, ...)

• Personne ne connaît la « bonne » réponse, ni les élèves, ni le maître, ni les chercheurs

• La réponse ne peut être qu’une estimation ou une fourchette

Au cours d’études empiriques antérieures menées auprès de publics très divers (Rauscher, Adjiage & Beliaeva, 2010 ; Adjiage & Rauscher, 2013), nous avons relevé trois grands types de stratégies qui toutes mobilisent l’usage de rapports exprimant soit une mesure soit une dilatation (Adjiage 2005; Adjiage & Pluvinage 2007).

Les deux premières stratégies prennent en compte directement le réel du parc d’attraction représenté sur la photo. Elles postulent implicitement l’existence d’une dilatation entre ces deux univers. La troisième stratégie en revanche amène à raisonner sur les objets de la photo puis à passer au réel du parc moyennant une dilatation explicite.

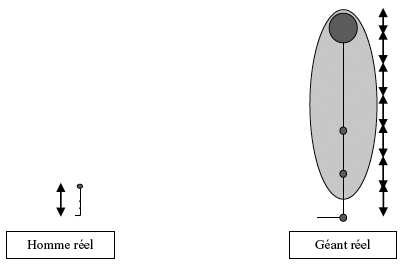
La stratégie 1 consiste à étalonner le géant au moyen d’un élément, apparaissant sur la photo, dont on est capable d’estimer les dimensions réelles. Un des hommes de la photo est le plus souvent choisi et la stature qu’on lui attribue est en général 1,80m, taille moyenne des Britanniques. Combien de fois peut-on reporter cet homme sur toute la hauteur du géant ? Le géant n’apparaissant pas en entier sur la photo, on ne peut répondre qu’indirectement à cette question, en substituant au corps du géant celui d’un individu accessible en entier (soi-même, un camarade, ...) au prix d’une hypothèse de similitude abusive : le géant est « fait » comme n’importe quel individu ou encore, en termes plus mathématiques, « le géant est le transformé par une dilatation d’un humain quelconque ». Or, sur la photo, un des hommes arrive à hauteur du mi-mollet du géant. Le rapport stature / mi-mollet, évalué sur le substitut choisi (soi-même, un camarade, ...), se conserve donc en passant au géant. Sa valeur, située entre 6 et 7, permet d’obtenir un encadrement de la stature réelle du géant.

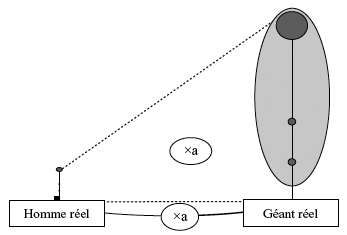
La stratégie 2 postule aussi l’existence d’une dilatation d’un homme quelconque, notamment celui de la photo, au géant. Mais elle permet d’éviter le recours à un substitut en utilisant le rapport de deux segments homologues (le plus souvent le rapport des semelles ou des mi-mollets mesurés sur la photo) pour trouver une approximation du rapport de dilatation. On applique alors directement ce rapport de dilatation à la stature réelle estimée de l’homme pour obtenir une approximation de la stature réelle du géant.

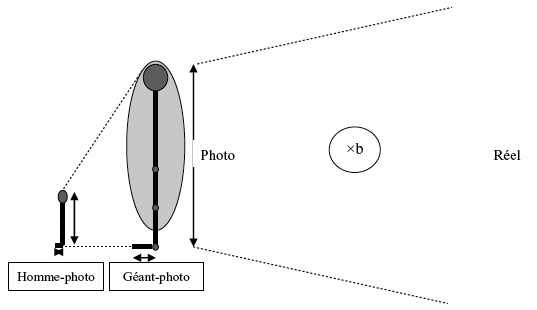
Comme les précédentes, la stratégie 3 suppose l’existence d’une dilatation de l’homme au géant. Contrairement à la stratégie 2 qui se fonde sur le calcul du rapport externe (coefficient de dilatation), celle-ci s’appuie sur la conservation du rapport interne de deux segments du corps, le plus souvent le rapport stature / longueur semelle, ces longueurs étant mesurées sur la photo. On en déduit par quatrième proportionnelle une approximation de la stature du géant - photo. En estimant ⁴ le rapport de la dilatation b qui fait passer de la photo au réel, on peut alors calculer une approximation de la stature du géant réel.

3. L’ETM générique en jeu dans la résolution du problème du géant

Le diagramme que nous présentons est adapté de Kuzniak (2011, p. 20). Il nous sert à décrire les ressources et le travail d’un individu, de quelque niveau qu’il soit, résolvant le problème du géant. Nous reprenons les trois genèses introduites par Kuzniak (2011), et nous instancions les trois composantes du plan épistémologique et les trois composantes du plan cognitif pour rendre compte de la spécificité de la tâche du géant. Nous décrivons ainsi trois pôles illustrés par des exemples. Chaque pôle est constitué d’une genèse et des deux composantes qu’elle relie. Cet ETM générique nous permettra de préciser des caractéristiques des ETM de référence et idoine, ainsi que des ETM personnels des élèves observés.

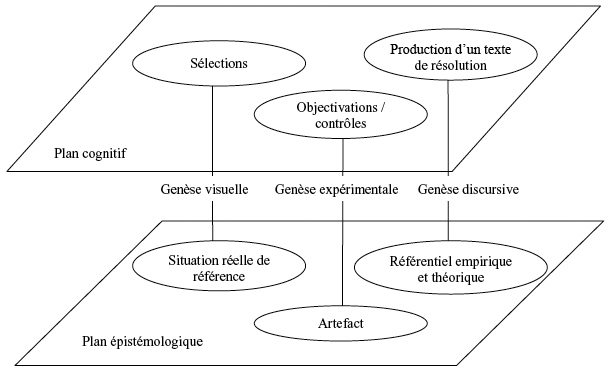
Pôle 1

Situation réelle de référence : la photo et le parc qu’elle représente

Genèse visuelle : traitement de l’image

Sélection : isoler et/ou relier des éléments saillants de l’image (on ne voit pas tout le géant ; il y a deux hommes ; un homme arrive au mi-mollet du géant ; la semelle est aussi grande que le mi-mollet...)

Pôle 2

Artefact : instruments de mesure ou de report ; Internet pour la taille moyenne d’un adulte ; l’élève qu’on prend comme modèle ; des textes - élèves de résolution ⁵

Genèse expérimentale : mesurages et mises en rapport ; navigation Internet ; sélection, comparaisons, déplacements, réorganisation d’écrits...

Objectivations / contrôles des éléments de preuve : rapport stature / mimollet ; modèle des proportions du corps humain ; complétude et cohérence de l’argumentation

Pôle 3

Référentiel empirique et théorique : connaissance du schéma corporel ; taille moyenne d’un adulte ; pertinence de unités utilisées ; proportionnalité

Genèse discursive : mise en rapport des repères visuels, des résultats expérimentaux, des repères empiriques et théoriques pour produire une preuve

Production d’un texte de résolution : écriture de la preuve.

4. L’ETM de référence

Dans quel ETM un expert résoudra-t-il le problème ? Son référentiel empirique et théorique devrait lui permettre d’appréhender instantanément la situation réelle de référence, constituée de la photo comme réduction de la partie du parc réel représenté. La question de la conservation des proportions de la photo au réel ne se pose sans doute pas. Elle est pour cet expert une donnée phénoménologique. Par ailleurs, un traitement visuel rapide de la photo, appuyé sur son référentiel empirique et théorique, devrait lui révéler que la résolution du problème passe par une hypothèse de proportionnalité. Même s’il est conscient que cette hypothèse est abusive, il sait aussi que trouver une solution acceptable passe nécessairement par des approximations. Le choix d’une des trois stratégies décrites en 2 est alors orienté par des éléments saillants et sans doute personnels du traitement visuel et/ou la plus ou moins grande correspondance de ceux-ci à des éléments du référentiel théorique (e.g. prise en compte d’un rapport externe ou interne). Une légère expérience de mesurage sur la photo ou sur lui-même, et la connaissance de la taille moyenne d’un adulte, qu’il peut sans doute trouver dans son référentiel empirique, suffiront à cet expert pour boucler le processus d’opérationnalisation de la situation (Julo, 1995, p. 50). Il lui reste à expliciter les éléments retenus pour former cette représentation et les traitements légitimes qu’il leur applique, puis de les organiser en un discours cohérent dans le cadre de limites qu’il précisera : hypothèse abusive mais raisonnable, approximation des mesures.

Ce qui caractérise cet ETM de référence est la richesse, la disponibilité et la précision du référentiel théorique et empirique qui orientent et légitiment les traitements visuels et discursifs, minimisent leur coût et permettent une sollicitation réduite du pôle expérimental.

5. Les ETM personnels initiaux des élèves observés

Au cours de la première séance du 23 mai (Tableau I en annexe), les élèves de la classe observée ont eu l’occasion de prendre connaissance du problème, d’envisager sa résolution et d’en débattre librement. Ils ont notamment entrepris les premières investigations de la photo : mesurer, dessiner des segments, etc. Par défaut de références empiriques, et aussi parce que les quelques éléments théoriques dont il dispose comme les schèmes de la proportionnalité sont à la fois mal stabilisés et peu reliés à son expérience personnelle, un enfant de 10-11 ans ne peut pas avoir la démarche d’un expert. Pour nombre des élèves observés, l’approche du problème a débuté par des évocations imaginaires : « C’est grand un géant, au moins comme un immeuble », avant de considérer non pas « un » géant mais le géant de la photo et de traiter objectivement les informations fournies par celle-ci. En fin de séance, les élèves ont été invités à produire un premier texte répondant à la question suivante : « Quelle est à ton avis la taille du géant ? Qu’est-ce qui te permet de dire cela ? ». Les productions ⁶ issues de cette séance nous permettent d’analyser les ETM personnels initiaux des élèves. Nous nous focaliserons sur la genèse visuelle en interaction avec le référentiel empirique et théorique, car ces éléments sont déterminants dans la résolution d’un problème dont l’énoncé repose essentiellement sur la photo d’un fragment de réel. Nous nous contenterons d’examiner ici six textes de résolution représentatifs de l’ensemble de la classe.

Ana

Jʼai fait le calcul de chaque partie du corps.

Moitié de la jambe : 9,5cm.

Pied : 8cm.

Moitié de la jambe : 9,5cm.

Autre pied : 8cm.

Autre moitié de la jambe : 9,7cm.

Autre moitié de la jambe : 9,7cm.

Bras : 9,0cm.

Autre bras : 9,0cm.

9,5+9,5+9,7+9,7+9+9+0,8+0,8=72,2m.

La taille du géant est de 72,2m [erreur de calcul]

Genèse visuelle

• Isolement sur la photo de deux segments particuliers du géant : demijambe visible et pied, à partir desquels on peut estimer les longueurs de chaque segment constituant la « taille »

• Ces segments ne sont pas rapportés à un étalon

Référentiel empirique

• Mesures directes au moyen d’un double - décimètre

• Evaluation des tailles des segments invisibles (autre moitié de la jambe, bras) à partir des segments visibles

• Théorème en actes : la « taille » est égale à la somme de certains segments du corps (pieds, jambes, bras) ; le changement d’échelle d’une feuille de papier au réel se fait en substituant les mètres aux centimètres

Référentiel théorique

• Problémes additifs

Cin

A mon avis le géant mesure 39,1m. Car déjà la taille de la [demi] - jambe mesure 9,7cm (9,7 m). Donc jʼai fait 9,7m+9,7m=19,4m et ça fait une jambe entier. Jʼai fait 19,4+19,4=39,1 [erreur de calcul] et ça fait un corps entier

Genèse visuelle

• Isolement sur la photo d’un segment du géant, la demi-jambe visible, à partir duquel on peut calculer la stature

• Ce segment n’est pas rapporté à un étalon

Référentiel empirique

• Théorèmes en acte : la longueur du corps entier peut-être engendrée à partir de deux doublages de la demi-jambe ; passage des cm au m (voir Ana)

• Mesures directes au moyen d’un double - décimètre

Référentiel théorique

• Problèmes de doublage

Ass

Les deux hommes mesurent à peu près 1m80 ou 1m70. La chaussure mesure à peu près 2m. Le géant mesure 6m quand je fais 2×3=6m, 2 car sa chaussure mesure 2m à peu près et quʼil manque 3 parties du corps : tête, jambe, ventre. Donc je fais 2×3=6 donc le geánt mesure 6m de haut par rapport aux deux hommes

Genèse visuelle

Isolement sur la photo la chaussure du géant par sa double pertinence :

• Segment du géant à partir duquel on peut reconstituer le corps entier

• Etalon car comparable ⁷ à un autre élément de la figure, un bonhomme, dont on peut estimer la taille

Référentiel empirique

• Théorème en acte : le référentiel empirique renvoie à un corps rudimentaire formé de trois parties considérées comme équivalentes (tête, ventre, jambes) pour le calcul de la taille

• Estimation de la taille d’un adulte

Référentiel théorique

• Problèmes multiplicatifs de type « un / plusieurs » : une partie mesure 2m, trois parties mesurent 6m (à la manière de : 1kg vaut 2€, 3kg valent 6€)

Neh

A mon avis la taille du géant serait 26m. Bin en fait jʼai vu sur la photo quʼil y avait des hommes et un pied de géant. Alors déjà je sais que la taille dʼun homme ça peut être entre 1m90 et 1m80. Donc le pied déjà, sa taille doit être 1m90 environs. Et après bin pour la taille du géant ça serait 26m environs

Genèse visuelle

• Isolement sur la photo des hommes en tant qu’étalons

• Isolement sur la photo du pied du géant

• Mise en rapport du pied avec l’étalon-homme

Référentiel empirique

• Estimation de la taille d’un adulte

Référentiel théorique

• Rien n’est explicité

Ber

A mon avis la taille du géant est de 144m [erreur de placement de virgule] Moi jʼai dit quʼil fallait faire 9×1,60 car 1,60 est la taille dʼun homme et 9 çà veut dire 9 hommes

Genèse visuelle

• Isolement sur la photo de l’homme en tant qu’étalon

Référentiel empirique

• Estimation de la taille d’un adulte

• Estimation du nombre de fois qu’un homme peut être reporté sur un géant sans expérimentation

Référentiel théorique

• Problèmes multiplicatifs de type « un / plusieurs » ou dilatation

Don

La taille du géant fait à peu près 5,40m car la taille dʼun homme mesure environ 1m80 puis je multiplie par 3,5 180×.....=500 180×2=360×1,5=540

Genèse visuelle

• Isolement sur la photo de l’homme en tant qu’étalon afin de permettre le calcul de la taille du géant par application d’un coefficient de proportionnalité

Référentiel empirique

• Estimation de la taille d’un adulte

Référentiel théorique

• Recherche d’un coefficient de proportionnalité

• Application d’un coefficient de proportionnalité

Remarque : Don, ayant sans doute identifié une situation de proportionnalité, part à la recherche d’un coefficient de dilatation de l’homme au géant (180 × …..=500 [nous n’avons pas d’explication sur l’origine du 500]) et finit par opter pour 3, 5

L’étude de ces six cas permet de dégager trois grandes approches :

• Un découpage du corps du géant en segments plus ou moins adapté au calcul de la stature (référentiel empirique d’Ana, Cin et Ass)

• Un étalonnage imaginé du corps du géant indépendamment de ses parties (référentiel empirique de Ber et peut-être de Neh)

• La recherche d’un coefficient de dilatation de l’homme au géant (référentiel théorique de Don)

Pour sortir de la photo et accéder aux dimensions réelles :

• Ana et Cin, qui restent polarisées sur le géant et lui seul, substituent de façon erronée les mètres aux centimètres (référentiel empirique : « sur la photo on mesure en cm, dans la réalité on mesure en m »)

• Neh, Ass, Ber et Don prennent en compte un élément extérieur au géant (un des hommes de la photo), estiment sa taille réelle et la mettent en rapport avec celle du géant (référentiel empirique ou théorique)

6. La question de l’ETM idoine

On distingue dans les procédures initiales décrites en section 5 du rudimentaire, de l’inachevé et de l’erroné. Nous faisons l’hypothèse que ces défaillances proviennent avant tout de ce que les genèses visuelles sont en liaison avec des référentiels empiriques et théoriques très rudimentaires ou erronés. Pourtant, la variété des mises en rapport de repérages visuels avec des références empiriques ou théoriques, mêmes défaillantes, contient en germe les possibilités de développer des procédures complètes et efficaces dans le cadre d’un ETM idoine.

Décrivons tout d’abord comment nous procéderions aujourd’hui, informés par notre analyse a posteriori, notamment en termes d’ETM, avant d’expliquer comment nous avons effectivement procédé dans le cadre de l’ingénierie.

6.1. Pistes a posteriori pour un ETM idoine

Un tel ETM devrait a minima comporter un référentiel théorique et empirique intégrant la dualité proportions vs dimensions absolues. En particulier dans le cas du corps humain, les unités fixes (cm, m) ne sont la seule façon de mesurer la taille. Rapporter celle-ci à un segment du corps, ou à un autre corps, peut être pertinent et déboucher sur des résultats surprenants : on peut être grand et avoir les mêmes proportions que quelqu’un de petit. A cet égard, nous suggérons deux pistes d’aménagement d’un ETM idoine permettant de faire rebondir les élèves sur leur ETM personnel.

La première piste consiste à donner de la consistance et de la cohésion au référentiel empirique en proposant par exemple un travail de reprise d’écrits entre pairs complété par un travail expérimental. En effet, la comparaison de quelques textes de résolution bien choisis par l’équipe de recherche aurait donné à voir aux élèves la variété des représentations du corps et leur potentiel informatif dans le calcul de la stature du géant. Suite à ce premier travail, une mise en questions de ces représentations du corps aurait été possible. Par exemple, les trois parties du corps ont-elles même longueur ? Pour mesurer la taille d’un individu doit-on additionner la longueur de toutes ses parties : les deux pieds, les deux bras, les deux jambes ? Combien de jambes, de demijambes rentrent dans un corps entier ? Ce qui est vrai pour le géant est-il vrai pour tout corps humain et à tout âge ? Le produit de ce travail aurait pu déboucher sur la prise de conscience des insuffisances de certaines représentations et, a contrario, sur les possibilités de se doter de représentations du corps pertinentes pour la résolution du problème (stratégie1).

La deuxième piste consiste à renforcer le référentiel théorique, en privilégiant l’appui sur les expérimentations de la première piste plutôt que des considérations formelles. Dans le cas de Don, il aurait été ainsi possible de l’aider à prendre en compte le rapport de deux segments homologues dans sa recherche d’un coefficient de dilatation (stratégie 2). Dans le cas d’Ana et de Cin, il aurait été judicieux d’amener ces élèves à s’interroger sur la pertinence du rapport 100 : 1cm sur la photo correspond-il à 1m dans la réalité ?

Pour résumer cela, nous pourrions dire que, suite aux constats d’insuffisances révélées par les premiers textes de résolution, il aurait été opportun d’amener les élèves à développer une genèse expérimentale pour recadrer et enrichir leur référentiel empirique et théorique, composante minorée dans les ETM personnels initiaux et spontanés des élèves. Dans les faits, nous avons en partie procédé comme cela, mais sans prendre suffisamment appui sur la richesse et la diversité des idées initiales.

6.2. L’ETM idoine effectivement mis en place

6.2.1. L’ETM idoine initial et la nécessité de son réaménagement

Lors des deuxième et troisième séances des 27 et 30 mai (Tableau I en annexe), les élèves ont eu à prendre connaissance de différents écrits de leurs pairs. Mais sans doute insuffisamment vigilants à ce que ces écrits nous révélaient de spécifique dans le rapport aux savoirs concernés, notre équipe a suivi la ligne générale de notre scénario : demander aux élèves d’une part d’élaborer un intervalle de plausibilité pour la taille du géant et d’en débattre, d’autre part de rédiger « des idées permettant d’avancer dans la résolution du problème ». Là où il aurait été souhaitable de pointer les insuffisances du référentiel théorique et empirique et d’y remédier, nous nous sommes trop vite placés dans une perspective de genèse discursive. Même si dans l’ensemble les idées émises furent encore ténues ou erronées, cette phase a néanmoins abouti à la production par deux groupes d’élèves en particulier de textes faisant apparaître quelques éléments pertinents de la stratégie 1. Voici ces deux textes.

Groupe Ber, Neh, Ela, Cin ; 30 mai

On dit que les mesures sont possibles et impossibles parce que je sais que sur la photo lʼhomme mesure à peu près la moitié du pied, je prends la moitié du pied et [au moyen dʼ] un stylo je regarde si cʼest la taille dʼun homme.... On fait ×9 car 9 personnes font environ tout le corps dʼun géant.

Groupe Cel, Bil, Ana, Don ; 30 mai

Dʼabord nous allons voir la taille de lʼhomme, elle est égale à 1m80. Ensuite nous allons prendre lʼhomme et on

le multiplie par 17 parce quʼon peut mettre 17 hommes à côté du géant. On a réussi cette étape car on a fait une expérience on a pris Bil puis une colle et on a fait 17 fois pour arriver jusquʼà la tête. [Un grand stick de colle est utilisé pour étalonner lʼélève Bil, le plus grand de la classe]

Lors des séances ultérieures du 6 et 9 juin (Tableau I en annexe), lors des débats qu’il a menés, le maître s’est essentiellement appuyé sur ces deux textes. Il a notamment a mis l’accent sur les idées d’étalonnage du géant passant par l’étalonnage du corps d’un élève, et donc sur une expérimentation directe. On pouvait alors espérer que nombre d’élèves s’empareraient des éléments de la stratégie 1 ainsi mis en évidence, les ordonneraient et les coordonneraient pour produire des textes de résolution acceptables.

Mais en fait, dans les rédactions individuelles clôturant la séance du 9 juin, on constate que les élèves se centrent quasi exclusivement sur les manipulations menées dans la réalité de la classe en oubliant leur rapport à la photo du géant et à la réalité qu’elle représente. Beaucoup d’objets d’étalonnage ont ainsi été choisis au hasard, le plus souvent sans rapport avec le mi-mollet (les sticks de colle, quelle que soit leur taille, ont été plébiscités puisque c’était le choix du groupe de référence) et encore moins avec l’homme de la photo. Le 9 juin, suite à des incitations enseignantes, les élèves réintègrent la réalité de la photo et du parc mais n’explicitent pas suffisamment les liens avec la situation d’étalonnage en classe. Ainsi, entre le 6 juin et le 9 juin, une véritable schizophrénie semble s’installer et on est loin de l’appropriation espérée de la stratégie 1.

Les textes de Neh et d’Ana sont représentatifs de ces cheminements et montrent la nécessité de réaménager l’ETM idoine pour dépasser ce blocage.

Neh, 6 juin

Je fais 19 colles et je mesure 1m65 environ.

Jʼai pris ma colle, je lʼai mis sur le pied et après jʼai compté jusquʼà ma tête, ça donne 19 colles.

Ma reponse :

Le géant mesure 32,35 m.

Ma méthode :

En fait, jʼai fait 19×1,65=32,35m. Jai pris la mesure de combien fait ma colle et ma mesure.

L’analyse correcte des rapports entre les personnages et le pied du géant, menée le 23 mai (5), disparaît ici au profit de manipulations. En effet, Neh ne considère que le rapport entre le tube de colle et elle-même et ne dit rien du rapport entre le tube de colle et la photo. De même, elle ne s’exprime pas sur le fait de prendre sa taille comme base de calcul de la taille du géant.

Neh, 9 juin

Je sais que la taille dʼun bonhomme cʼest 1,80m, je sais que si je prends un objet qui va à la moitié du mollet et que je le reporte ça fera 6× ma taille donc ça va faire pareil pour le géant.

La résolution du problème : 1,80×6=10,80. Le géant mesure 10,80m

Neh arrive à un résultat plausible. Par rapport au texte précédent on voit des ponts établis entre la situation d’étalonnage en classe et la photo : « ça va faire pareil pour le géant ». Mais ces articulations ne sont pas encore explicitées clairement. En particulier, le choix du mi-mollet reste opaque et son rapport avec la taille d’un homme n’est pas évoqué.

Le cas d’Ana montre de façon plus évidente encore ce clivage entre la situation de la photo et la situation d’étalonnage en classe.

Ana, 6 juin

Je vais prendre différente chose comme lʼéquerre, un tube de colle, lʼeffaceur et je vois si ça fait la même chose et je vais comparer :

Pour moi :

une règle : 4

colle : 15

équerre 8

Pour Naï :

une règle : 5

colle 15,30

équerre : 8

Jʼai fait avec Naï, on a fait avec Iʼéquerre, la règle et la colle. Jʼai comparé et comme elle est plus grande que moi, ce nʼest pas pareil. Je prends la colle et je mesure chaque partie de mon corps.

Je pense que le géant mesure 16m car jʼai mesuré chaque partie de mon corps et jʼai multiplié.

Ana procède à une série d’étalonnage de sa taille et de celle de son amie Naï sans donner du sens à ce travail. Le résultat final est déconnecté de ces expériences et semble faire référence à sa procédure du 23 mai (5).

Ana, 9 juin

Je fais 6×1,80=10,80, jʼai fait 6×1,80 pour trouver la taille du géant, jʼai utilisé la moitié de la jambe et il faut 6 fois la moitié de la jambe.

On voit bien réapparaître la réalité du parc mais aucune explication n’est donnée sur le rapport 6 ou la signification du 1,80. Aucun lien avec la situation d’étalonnage en classe n’est fait. A ce moment-là, la compréhension de la stratégie 1 par Ana semble encore hors d’atteinte.

6.2.2. L’ETM idoine réaménagé par une pratique écrite de l’écrit

Afin de débloquer la situation, l’équipe a décidé d’agir sur le pôle expérimental de l’ETM idoine, mais pas à la manière décrite en 6.1 dont l’occasion avait été manquée. Les textes du 9 juin ne permettaient pas de décider si les élèves ne faisaient que répéter mimétiquement les avancées de la classe ou s’ils exprimaient la partie émergée d’un raisonnement plus abouti. Pour lever cette ambiguïté, nous avons mis en place le 17 juin un dispositif destiné à favoriser l’explicitation de leur argumentation. A cet égard, nous avons mis à la disposition des élèves un matériel (artefact) qui leur a permis de développer une « pratique écrite de l’écrit ». Opposée à « une pratique orale de l’écrit » (Duval, 2001, p. 191), cette dernière est bien spécifiée par Tanguay (2005) comme étant :

[…] faite de pauses, de retour sur les propositions déjà énoncées, de réaménagements et simultanéisations (pour rapprocher des propositions ou blocs de propositions non contigus dans le texte), de recul, d’appréhension globale (pour saisir certains éléments de macro-organisation) ; bref, de réflexion. Toutes choses que ne permet pas cette « linéarisation de la pensée » (Duval 2001, p.191) imposée par une pratique orale du texte, faite de fluence, de séquencialité, d’irréversibilité. À travers une telle « pratique écrite de l’écrit », l’élève produit le texte de démonstration non plus à des fins de communication, mais pour « en contrôler et la validité et l’absence de lacunes. ». (p.2)

Pour offrir cette possibilité d’expérimentation et de construction aux élèves, nous leur avons donné à examiner quatre textes, issus de leurs rangs, rédigés lors de la séance du 9 juin (Tableau ii en annexe) et sélectionnés par l’équipe de recherche. Ces textes ont été choisis car on peut trouver dans leur réunion la quasi - totalité des éléments d’un raisonnement rigoureux. Même les textes les plus incomplets apportent des contributions qui ne figurent pas nécessairement dans les autres textes.

Dans une perspective d’expliquer sa solution à des élèves d’une autre classe de CM2, la consigne était d’abord de noter « ce qui est bien dans chacun de ces textes et ce qui manque pour comprendre la solution. » puis de proposer collectivement un cahier des charges pour une solution et enfin de rédiger individuellement sa solutio

Les élèves ont alors effectivement mis les textes en questions, repéré la présence ou l’absence d’éléments pertinents, relevé des imprécisions, proposé des améliorations (genèse expérimentale). Ils se sont bien engagés dans une pratique écrite de l’écrit. Ce travail a sans doute été déterminant pour amener deux tiers d’entre eux à expliciter les éléments et les articulations d’un raisonnement complet, comme le montrent les textes de résolution de Neh et Ana, une nouvelle fois représentatifs de ces cheminements.

Neh, 17 juin

Puisquʼon nʼa pas le géant sous nos yeux, alors on prend un objet qui fait la moitié du mollet. Puisque sur la photo on voit que lʼhomme fait le mi-mollet du géant, alors on imagine que je suis le géant et que lʼhomme cʼest lʼobjet. Après je le reporte de toute ma taille et ça fait 6 fois. La taille dʼun homme cʼest 1,80m, alors je fais 6×1,80=10,80m

Réponse : le géant mesure 10,80m

Le lien ténu, présent dans le texte du 9 juin de Neh, entre les actions menées en classe et la situation évoquée par la photo (« Ca va faire pareil pour le géant »), est à présent développé et la démarche de modélisation bien explicitée via une séparation claire mais articulée entre le modèle (son propre corps) et le représenté (le géant).

Ana, 17 juin

On a pris un élève de la classe. Puis on a pris un objet pour faire les hommes. Il faut prendre un objet puis le faire jusquʼà ce quʼon arrive à la tête. Il faut 6 ou 7 fois lʼobjet pour arriver à la tête et pour trouver la taille. Ex. il y avait des hommes à côté du pied du géant. On les a utilisés pour trouver la taille du géant. Un homme mesure à peu près 1m80. On prend 1m80 et combien de fois on a pris lʼobjet pour arriver à la tête. 1,80×6=10,80

Le texte du 9 juin évoquait quelques actions menées en classe mais ne faisait aucun lien avec la situation évoquée par la photo. Dans le texte du 17 juin, l’ensemble des éléments d’un raisonnement complet apparaissent presque tous mais ils sont désordonnés. Ana produit un texte intermédiaire, où elle tente d’assembler les pièces d’un puzzle, sans toutefois y parvenir totalement: « on a pris… puis on a pris... on les a utilisés…il faut… ».

Globalement, deux tiers des élèves ont tiré profit du traitement des écrits de leurs pairs pour combler les lacunes de leur propre texte et réorganiser ceux-ci pour produire un raisonnement acceptable. Cette genèse expérimentale particulière leur a permis de mettre en relation les repères visuels de la photo, les expérimentations menées en classe et les éléments pertinents du référentiel empirique, et donc de développer leur genèse discursive.

Mais il faut aussi évoquer le tiers des élèves qui n’ont pas produit des textes de résolution satisfaisants. Leurs textes montrent en général qu’ils n’ont pas compris les éléments clés de la résolution du problème, notamment ceux liés à la modélisation. Voici l’exemple de Naï qui illustre bien cela.

Naï, 17 juin

On prend 1,80m×7. 1,80m parce que cʼest la taille dʼun homme en général, 7 parce que quand on prend on objet qui nous arrive au mi-mollet et quʼon le reporte sur nous ça donne 7 fois.

Calcul : 1,80×7=12,60

(Quand il y a des personnes qui reportent un objet ça donne 6 ou 7 fois mais moi jʼai décidé de prendre 7 parce que cʼest plus grand que 6 et je me dis que cʼest mieux de prendre la plus grande mesure (7) car on parle dʼun géant)

Aucun lien n’est fait entre le modèle (un élève) et le géant d’une part, entre l’objet reporté et l’homme de la photo d’autre part. De plus, Naï semble penser qu’il n’y a que deux coefficients possibles, 6 et 7, et choisit 7 parce qu’il débouche sur « la plus grande mesure», donc plus conforme à la taille d’un géant… Ces nombres ne sont pas interprétés comme des coefficients de proportionnalité mais comme des absolus. Nous voyons ici que les éléments du référentiel empirique sont reliés de façon erronée aux éléments d’un référentiel théorique défaillant dans l’ETM personnel de l’élève.

7. Conclusion

Dans une étude antérieure consacrée à l’observation de professeurs enseignant la géométrie au collège et au lycée (Kuzniak & Rauscher, 2011), la notion d’ETG s’était révélée pertinente pour voir dans quelle mesure ils tiennent compte ou pas des espaces de travail personnels des élèves pour permettre à ces derniers d’avancer dans les apprentissages. Ici, notre étude révèle le potentiel du cadre ETM pour analyser l’activité mathématique des élèves confrontés au problème du géant et parallèlement pour élaborer ou rectifier des modalités d’enseignement en conséquence. Ce cadre nous a en effet permis de revisiter notre ingénierie et de mettre au jour ou de réinterpréter trois points importants de celle-ci.

• Le premier de ces points concerne la prise en compte des ETM personnels initiaux des élèves qui révèle avant tout des déficits précis du référentiel empirique et théorique. En s’appuyant sur ceux-ci, nous avons pu dégager a posteriori des pistes pour développer une genèse expérimentale dans le cadre du référentiel idoine

• Le deuxième point concerne l’interprétation des blocages qu’ont connus les élèves lors des séances du 6 et 9 juin en termes de dissociation des genèses visuelle et expérimentale, en bonne partie dues à la centration prématurée de notre scénario d’enseignement sur la genèse discursive

• Le troisième de ces points concerne la réussite de deux-tiers des élèves à produire une genèse discursive efficace en fin de parcours que nous expliquons maintenant par l’intégration, grâce à une pratique écrite de l’écrit, des genèses visuelle et expérimentale, cette dernière enrichissant, stabilisant et rendant plus disponible le référentiel empirique et théorique

De façon plus large, on peut penser que la notion d’ETM est un outil pertinent pour objectiver et réaliser le lien nécessaire entre la vigilance épistémologique et la vigilance didactique à exercer dans des situations de problèmes de modélisations proposés à de jeunes élèves. La perspective de notre étude serait ici de développer un cadre ETM de la modélisation à ce stade de la scolarité (10-11 ans) ou même de l’étendre à d’autres niveaux de scolarité. Le diagramme de la Figure 5 pourrait être une base de travail pour un tel projet. Nous nous plaçons dans les limites d’une « initiation à la pratique de la modélisation » (Brousseau, 2003, p. 25) que nous résumons en quatre points issus de Legrand (Brousseau, 2003, p. 34) :

• Partir d’un réel plus ou moins délimité et d’une question

• Choisir les objets et paramètres pertinents

• Construire des règles traduisant les relations entre objets

• Construire un modèle (monde imaginaire ou réel reconstruit) pertinent vis à vis du questionnement initial et assez mathématisé pour que l’on puisse calculer, comprendre comment ça marche

Dans ce contexte, les genèses visuelle et expérimentale et leur articulation nous semblent être les composantes majeures de l’ETM idoine, en tout cas dans le travail d’approche des élèves indispensable pour aborder la phase finale de la genèse discursive. Nous insistons aussi sur le rôle majeur que devrait jouer la pratique écrite de l’écrit à l’intérieur de la genèse expérimentale dans le cadre d’une telle ingénierie.

Referencias

Adjiage, R. (2005). Diversité et invariants des problèmes mettant en jeu des rapports. Annales de Didactique et de Sciences Cognitives, 10, 95–129.

Adjiage, R., & Pluvinage, F. (2007). An experiment in teaching ratio and proportion. Educational Studies in Mathematics, 65, 149–175.

Adjiage, R., & Rauscher, J. C. (2013). Résolution d’un problème de modélisation et pratique écrite de l’écrit. Recherche en Didactique des Mathématiques, 33 (1), 9-44.

Bkouche, R., Charlot, B., & Rouche, N. (1991). Faire des mathématiques : le plaisir du sens. Bibliothèque Européenne des sciences de l’Education. Paris, France: Armand Colin.

Brousseau, G. (2003). Quels types de savoirs mathématiques utilise-t-on dans la modélisation ? In Raoult J. P. (Ed.), La modélisation, recueil des contributions présentées le 26 novembre 2003 (pp.13–17). Paris, France: IREM de Paris 7.

Duval, R. (2001). Écriture et compréhension : Pourquoi faire écrire des textes de démonstration par les élèves ? In Barbin E., Duval R., Giorgiutti I., Houdebine J., Laborde C. (Eds.), Produire et lire des textes de démonstration (pp. 183-206). Paris, France: Ellipses.

Julo, J. (1995). Représentation des problèmes et réussite en mathématiques. Rennes, France: Presses Universitaires de Rennes.

Kuzniak, A. (2011). L’Espace de Travail Mathématique et ses genèses. Annales de Didactique et de Sciences Cognitives, 16, 9–24.

Kuzniak, A., & Rauscher, J. C. (2011). How do Teachers’ Approaches on Geometric Work relate to Geometry Students’ Learning Difficulties? Educational Studies in Mathematics, 77 (1), 129–147.

Legrand, M. (2003). Différents types de modélisation dans l’enseignement. In Raoult J. P. (Ed.), La modélisation, recueil des contributions présentées le 26 novembre 2003 (pp.13–17). Paris, France: IREM de Paris 7.

Peter - Koop, A. (2004). Fermi problems in primary mathematics classrooms: Pupils’ Interactive Modelling processes. In Mathematics education for the third millennium: Towards 2010 (Ed), Proceedings of the 27th annual conference of the Mathematics Education Research Group of Australasia, Townsville (pp. 454–461). Sydney: MERGA.

Rauscher, J. C. (2006). L’écriture réflexive au centre de l’activité mathématique dans la résolution de problèmes de proportions. Annales de Didactique et de Sciences Cognitives de l’IREM de Strasbourg, 11, 75–102.

Rauscher, J. C., Adjiage, R., & Beliaeva, T. (2010). Modélisation et écrits réflexifs : des outils pour apprendre ? Réflexion à partir d’une expérimentation en CM2. In Danos P. (Ed.), Actes du 36ème Colloque COPIRELEM. Auch 2009, L’enseignement des mathématiques à l’école : où est le problème ? [Cédérom]. Paris, France: ARPEME.

Tanguay, D. (2005). Introduction. In Tanguay D. (Ed.), Actes du colloque du Groupe des didacticiens des mathématiques du Québec GDM 2005 (pp. 1–4). Montréal : UQAM.

Notas

1 Apprentissages en contexte et didactique des disciplines, groupe de la Vie Scientifique de l’IUFM de Université de Strasbourg alors composé de : Robert Adjiage, Tatiana Beliaeva, Virginie Deloustal - Jorrand, Jean - Claude Rauscher, Marie - José Remigy, Nicolas Séchaud.

2 Photographie copiée de http://www.problempictures.co.uk/, avec l’aimable autorisation des auteurs.

3 Fermi était connu pour poser à ses étudiants des problèmes qui ne pouvaient être résolus qu’au prix d’une estimation raisonnable comme : « Combien y a-t-il d’accordeurs de pianos à Chicago ? ».

4 Le coefficient b peut être obtenu à partir du rapport de deux segments homologues dans la dilatation qui fait passer de la photo au réel, e.g. rapport de la stature réelle (estimée) d’un des hommes en train de discuter à sa stature-photo (mesurée directement sur la photo).

5 La reprise de textes de résolution occupe une place importante dans notre ingénierie, en tant qu’outil de travail réflexif pour les élèves (voir 6.2.2).

6 Les conditions dans lesquelles ces productions ont été réalisées sont décrites dans le Tableau i en annexe.

7 Il semble qu’Ass ait estimé que la chaussure du géant est un peu plus grande qu’un des deux hommes d’où le 2m.