1. Introduction

Teaching geometry so that students develop meaningful geometrical knowledge requires careful observation of the ways students gain understanding of various geometrical topics (Battista, 1999). Thus, mathematics teachers need to investigate and identify how students acquire geometrical knowledge. In order to attain more adequate information about children’s geometrical knowledge development, it is important for teachers to recognize that the body, and especially its gestures, could be considered as a reference point and as a source of experiences to reason, learn and grow (Kim, Roth, and Thom, 2011). Furthermore, when children are asked to explain their behavior, their verbal expressions may not capture all components of their understanding, as a result of difficulties to tap some knowledge through verbal expressions (Ericsson and Simon, 1980). Therefore, gestures can be another possible “location” where the generation of children’s mathematical thinking and, thus, geometrical knowing can be observed.

Compared to other topics in mathematics, the role of gestures in early geometry learning has received limited attention. The purpose of the present study is to explore kindergartners’ gestures, from a cognitive point of view, in a geometrical semiotic transformation activity of communicative character in two different types of space of constructed representation (SCR).

2. Theoretical framework

In the present paper we use as explanatory frameworks Duval’s cognitive approach to geometry learning (1995, 1998), the Geometrical Work Space (GWS) (Kuzniak, 2009; 2012) and previous research on gesture (McNeill, 1992) and its role in mathematics learning (Radford, 2009).

2.1. Duval’s cognitive model of geometrical reasoning

Semiotic representations in elementary geometry are produced within three different registers: shape configuration, linguistic statements and numerical values and / or symbolic formulae. In addition, geometrical thinking involves three kinds of cognitive processes, that is, visualization, construction and reasoning processes (Duval, 1998).

In this study we concentrate on the register of geometrical figures (or shapes) and on the cognitive process of visualization (Duval, 1998). Visualization includes the recognition of figural units which can be identified in a configuration of shapes as well as figural treatment. Recognizing figural units in the early years is based on the perceptual apprehension of figures, while figural treatment is a major component of the operative apprehension of geometrical figures (Duval, 1998). Perceptual apprehension refers to the recognition of a shape in a plane or in depth, the recognition of shapes in a perceived figure and the naming of shapes. Operative apprehension depends on the various ways of modifying a given figure: the mereologic, the optic and the place way. The mereologic way refers to the division of the whole given figure into parts of various shapes and the combination of them in another figure or place of figures (reconfiguration), the optic way is when one makes the figure larger or narrower, or slant, while the place way refers to its position or orientation variation. Each of these different modifications can be performed mentally or physically, through various operations. The shape configuration problem that is used in this study is closely linked to perceptual and operative apprehension of geometrical shapes. The shape configuration problem in this study also involves discursive processes by the solver, and an explanation specifically about which shapes to use and about their proper positions and orientations in the composite figure. Thus, the geometrical activity used in this study incorporates two registers of representation, shape configuration and linguistic statements, as well as conversion processes between them. Furthermore, the activity used in this study takes place within ‘microspace’ (Brousseau, 1983). Microspace refers to a space of interactions tied to manipulation of small objects (Brousseau, 1983). The geometrical representation that is included in this study is constructed in two different types of micro - space: objects (2D-shapes) made of paper and computer screen. These SCRs, as we called them earlier, are likely to differ in the processes they stimulate to the students while constructing a composite geometrical representation with shapes. This could be a consequence of the use of technological tools that are included in the applet for the manipulation of the geometrical figures (Duval, 1995).

2.2. Gestures in mathematics learning

Mathematical thinking cannot be reduced to working with abstract mathematical ideas. It is mediated by, but also located in, body, artifacts, and signs. This means that semiotic and physical resources as well as bodily activity, including gestures, are indispensable components of thinking and conceptualization at any level of development (Radford, Bardini, Sabena, Diallo, and Simbagoye, 2005). Because of their embodied character, gestures can play an objectifying role (Radford, 2003), that is, they serve as a representational tool of various mathematical ideas through which learners can gain a deeper level of consciousness of their culturally and historically developed meaning (Radford et al., 2005). In this way, learners can also communicate mathematical concepts more easily (Gallese and Lakoff, 2005; Nemirovsky and Ferrara, 2009).

According to McNeill (1992, p. 35), “[s]peech and gesture are elements of a single integrated process of utterance formation in which there is a synthesis of opposite modes of thought - global - synthetic and instantaneous imagery with linear segmented temporally extended verbalization”. This means that speech consists of segments that are produced linearly through time, whereas gesture is immediate, represents an image which depends on the whole and cannot be decomposed into parts with isolated meanings. This view, on the one hand, suggests that the gestures’ cognitive potential can be analyzed and understood only in the context of their interaction with other modalities (Radford, 2009) and primarily with language. On the other hand, it is suggested that the contribution of gesture to mathematical understanding, which almost always requires both analytic thinking and imagery, is distinct from the role of other modalities.

McNeill (1992) proposes four categories of gestures regarding their meaning:

1. 1. Deictic gestures, pointing movements to existing or virtual objects and actions in space. For example, think of a child in a kindergarten who is asked by the teacher where the puppet is and the child says “Under the table”, using a deictic gesture to indicate the specific location.
2. 2. Iconic gestures which are closely related to the semantic content of speech, that is, they visually represent the content of concrete entities and actions. For example, think of a child who is describing a spatial construction to a conversation partner and she makes a gesture of a round line in the air for the shape of cylinder.
3. 3. Metaphoric gestures, which represent an image of an abstract object or idea. For example, a speaker divides the space of gesture in front of him to illustrate the notions ‘good’ and ‘bad’ by moving his hands respectively to the right and to the left (or in the opposite direction) (McNeill, 1992).
4. 4. Temporal highlighting gestures, simple repeated gestures used for emphasis. They are used by the speaker to highlight something he / she feels is important, for example, when he / she first mentions a character of a story (McNeill, 1992).

2.3. The Geometrical Work Space (GWS) for the solution of the geometrical configuration problem in the present study

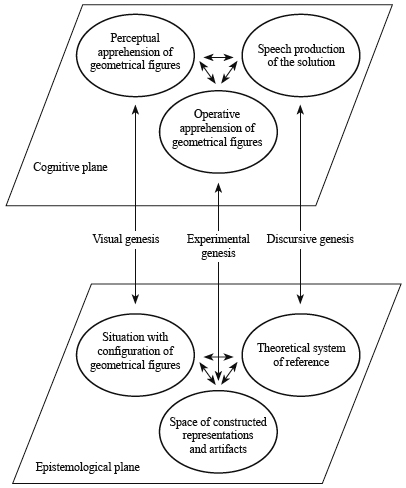
The present study is based on a geometrical activity which offers a place that is organized to enable children (in this study, one child) to solve a geometrical problem. This place can be termed as Geometrical Work Space (Kuzniak, 2012). As the geometrical activity used in this study has a mathematical dimension, it is inevitable to comprise of three interacting components which can describe the epistemological level of GWS: real space, artifacts, and a theoretical frame of reference. Furthermore, since a main focus of the study is to understand how children use geometrical knowledge to solve the problem included in the geometrical activity, it is essential to consider in our analysis the three processes involved in the GWS at the cognitive level: visualization, construction and reasoning. Working coherently and efficiently in the GWS entails an articulation between the epistemological level and the cognitive level. This process depends on the transformations of the epistemological components into objects that can be used meaningfully in the cognitive processes of individuals. These transformations are found in three fundamental geneses: semiotic - figural, instrumental and discursive (Kuzniak, 2012).

In this study, the three dimensions introduced by Kuzniak (2012), including the epistemological components, the cognitive components and geneses, are adapted to meet the specific characteristics of the activity and of the young age level under study (kindergarten) and therefore some components of these dimensions are renamed. For example, the three cognitive processes involved in the particular geometrical activity are drawn from Duval’s (1998) cognitive approach for the apprehension of geometrical figures (see above). The modified components are depicted in Figure 1, which is adapted from the GWS in Kuzniak (2012). This figure shows the resources and the work of an individual while solving the geometrical configuration problem proposed in this study (see Method section for the particular task) or other similar problems. All the dimensions of the GWS for this activity and their components are also described below. It should be noted that the particular activity is situated within the paradigm of Geometry I as it finds its validation in the material and tangible world (Kuzniak and Rauscher, 2011).

First dimension

Situation with configuration of geometrical figures (geometrical representation): the outline of geometrical figures and the available geometrical shapes (see Figure 2).

Visual genesis: observation and visual treatment of the geometrical configuration (e.g., recognizing that the configuration is made up of geometrical shapes placed in specific positions and orientations) and of the individual geometrical shapes (e.g., recognizing that individual geometrical shapes can be parts of the configuration if combined appropriately).

Perceptual apprehension of geometrical figures: recognition and naming of geometrical shapes that fit in the outline and specification of their position.

Second dimension

SCRs and artifacts:1) First SCR, that is, computer, mathematical applet, tools available in the applet (e.g., spin tool), 2) Second SCR, that is, paper material (e.g., geometrical shapes and the outline of the composite figure made of paper).

‘Experimental’ genesis: manipulation of geometrical shapes through child’s verbal instructions

Operative apprehension of geometrical figures: geometrical reconfiguration, place way modifications (rotation and translation) of shapes to fit in the outline.

Third dimension

Theoretical system of reference: knowledge of two dimensional geometrical shapes, geometrical transformations (rotation and translation) of shapes, spatial relationships (besides, right, left, on, under, etc).

Discursive genesis: Speech production about the visual recognition of shapes and their manipulation.

Discursive reasoning for the solution of the problem: Production of coherent instructions for combining the geometrical shapes to compose the larger composite figure, implicit use of the notion that a shape remains the same in different positions and orientations.

The present study addressed the following research questions about early geometrical thinking evoked by two types of SCR, namely on the computer, with the use of a digital mathematical applet, and on paper: (a) What are the types of gestures that are produced in a geometrical semiotic transformation activity including a two - dimensional shape configuration problem? (b) What are the interrelations between geometrical figure apprehension processes and gesturing? Investigating these questions may enable us also to gain useful understanding about young children’s personal work space (Kuzniak, 2012) while dealing with such geometrical activities, with a focus on gestures and their role in geometrical work.

3. Method

3.1. Nature of the study

To address the research questions it is essential to acquire a profound insight into the phenomenon of gestures in early geometry learning. Radford (2009, p. 124) pointed out that “[t]o better weigh the role of gestures and bodily actions in mathematics cognition, more detailed investigations are required.” Therefore, we carried out a qualitative single - case study, in which we examined one child while interacting with her kindergarten teacher in a geometrical activity, in the context of two different SCRs. In particular, a 5-year-old girl was observed. She is a student in a public kindergarten, in Larnaca, Cyprus.

3.2. Activity and procedure

The activity that was used included a shape configuration problem (shape puzzle) in two different SCRs, namely, on the computer, with the use of a digital mathematical applet, the Patch Tool, which is available on the Illuminations Website by the National Council of Teachers of Mathematics (NCTM) (http://illuminations.nctm.org/ActivityDetail.aspx?ID=27) and on the paper, respectively. The goal of the activity in each SCR was for the child to give the right instructions to the experimenter so that the experimenter could fill a composite figure with a given outline, by selecting appropriate shapes and by putting them in the proper place and orientation. Although the puzzle suggests the placement of each shape by including internal lines, each shape does not represent a unique role in the configuration (e.g., one shape for each part of the puzzle) and does not touch other shapes only at a point. This means that several shapes are combined by matching their sides to make one part of the puzzle (Clements and Sarama, 2009). To accomplish the task the child needed to activate the following competences: recognizing a shape and indicating how to place it with respect to its orientation and its position relative to other shapes in the configuration.

The focus of our study by selecting this task and developing this activity was not to find out whether the child could solve the problem successfully. The rationale behind the design of this activity was based on gaining access to the child’s mental processes when filling a shape configuration through her verbal and gestural acts. For this reason, the researcher encouraged the child to express her thinking by probing and asking questions to the child throughout the whole activity without providing any guidance for the solution of the puzzle.

Concerning the SCRs, our focus was to find out whether the interaction of the same child with a different SCR when dealing with the same task would substantially differentiate (or not) her geometrical thinking as “materialized” through her gestures and words. At the first SCR, the computer, the user (in this study the experimenter following the instructions of the child) could move a shape using the mouse, rotate a shape using the spin tool and delete a shape using an eraser. These operations could be applied, also, in the second SCR (paper) by the experimenter, by using his hands. As shown in Figure 2, the same outline of composite figure and the same shapes (triangle, rhombus, square, trapezoid and hexagon) were used in both SCRs.

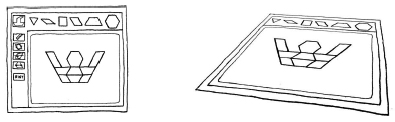
We admit, though, that having the computer activity first might have an effect on the child’s behavior in the paper activity that followed, but we tried to diminish this effect by having an interval of two weeks between the two activities. Furthermore, if such an effect still occurs, we would consider it as an indication that the child, affected by the dynamic character of the computer, may be able to transfer the processes developed through gestures and language from using the computer on the paper. This is an interesting indication for further study, which would not occur if the reversed order of SCRs was applied instead (first: paper, second: computer). This is the reason we selected the particular order of SCRs, even though the examination of such an indication is beyond the aims of the present case study.

Before starting each activity, the experimenter explained the rules to the child and the goal of the game. Specifically she told the child that she must give her instructions so that the shapes she had in front of her could be combined to match the provided outline of the composite figure. In addition, on the computer she explained to the child the functions of the spin tool (i.e., to turn the shape) and the eraser (i.e., to remove the shape).

3.3. Data collection and analysis

To examine the child’s gestures and language, her reactions and utterances during her participation in the activity were video - recorded. Guided by our research questions and theoretical framework, we conducted a microgenetic analysis (Siegler, 1995) of the child’s utterances and gestures during the activity in both SCRs. Specifically, we carried out an intensive analysis of the observed behavior of the child (Lavelli, Pantoja, Hsu, Messinger, and Fogel 2005). It is our contention that this microgenetic approach can shed some light on the processes the child goes through while thinking of, and communicating concepts related to geometrical figures during her interaction with each SCR in a shape configuration problem. In carrying out the microgenetic analysis, we focused on the child’s use and coordination of two semiotic resources, namely, spoken words and gestures, in connection to the geometrical representations provided at each SCR.

4. Results

The total number of gestures produced by the child while acting in the activity was 47 on computer, and 38 on paper. On the computer 21 gestures were identified as deictic and 26 gestures were categorized as iconic. On paper, 10 gestures were iconic and 28 gestures were deictic. The duration of the activity was 13 min and 24 seconds on the computer and 10 min and 9 seconds on paper.

4.1. Gestures’ categorization

In order to address the first research question about the types of the kindergartner’s gestures while dealing with the shape configuration problem, we categorize the gestures the child produced on the two SCRs according to the classification that was proposed by McNeill (1992). The child was found to produce two kinds of gestures, namely deictic and iconic gestures, in each SCR.

4.1.1. Types of gestures on the computer

Below we first give the child’s constructed representation in the first activity (see Figure 3). The figure is followed by an extract of the child’s talk with the experimenter and gestural activity.

1 E: I would like you to show me the first shape that you want to use.

2 C: I want to start with this shape (points her finger to the rhombus).

3 E: And where do you want to place it?

4 C: I want to place it here (points her finger down, on the right side of the figure).

5 E: Ok, I am going to start the game. This one is a rhombus (puts the shape in the indicated place). Is it right how I put it?

6 C: No.

7 E: What do you want to do?

8 C: You have to turn it (makes a rotation with her pointing fingers, using both of them as moving points).

9 E: Helen, you are amazing. I will turn it (makes a rotation using her pointing fingers). I am taking this tool and I am starting to turn it. Is it right here?

10 C: No, you have to turn the shape once more (makes a rotation with her pointing fingers, using both of them as moving points).

11 E: Once more. Is it right?

12 C: You have to turn it again (makes a rotation with her pointing fingers, using both of them as moving points).

13 E: Ok, I will turn it again. Is it right?

14 C: Yes.

15 E: Wonderful. Is the place absolutely right?

16 C: No.

17 E: What do I have to do?

18 C: You have to turn it on the left (puts her palms opposite to one another in a vertical direction and she moves them on the left).

19 E: On the left (shows with her pointing finger on the left). Nice. Is it right?

20 C: Yes.

21 E: Nice. We have placed the shape on the right location. Let’s place the second shape. Tell me, show me.

22 C: (She shows the trapezoid with her pointing finger).

23 E: Do you know its name?

24 C: Yes I know it…

25 E: It’s a tr…

26 C: A rectangle.

27 E: No, it’s a trapezoid.

28 C: The trapezoid.

29 E: Excellent. So, I am choosing a trapezoid. And, where do you want to place it?

30 C: Here (shows with her pointing finger the location on the bottom of the figure).

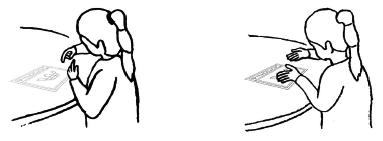
When the child gestured about the geometrical transformations (i.e., rotation and translation of the shape) in order to fill the composite figure, these gestures were of iconic character. An example concerns the rotation (lines 9-10), for which the child made a rotation using her pointing fingers as moving points (see Figure 4a). A second example refers to the translation of the shape. Specifically, when the child wanted to move a shape, she moved her hand from the direction that she wanted to displace a shape to the direction that she wanted to place the shape (lines 23-24, see Figure 4b).

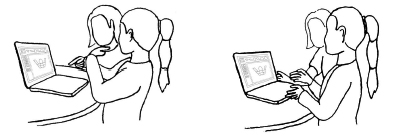
The verbal expression “turn” was usually accompanied with the iconic gesture of rotation (line 13). However, the same verbal expression was used by the child when she talked about a shape’s translation. In particular, many times when the girl wanted to move a shape from one place to another she used the word “turn” (lines 23-24). In these cases the role of gestures was very significant for the partners in communication, the experimenter and the child. On the one hand, through gesture, the experimenter gained a clearer understanding about how the child wanted to manipulate the shape in order to fit on the composite figure. On the other hand, the child, despite her difficulty to describe verbally the particular geometrical transformation, using gesture, began to objectify and achieve to communicate this mathematical idea.

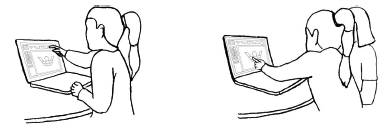
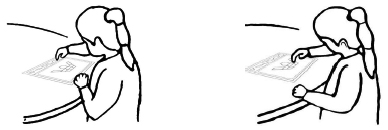
To indicate the selected shape and the place that the shape could fit, the child always produced deictic gestures, stretching her hand and pointing with her pointing finger the shape or the location (lines 29 and 37, see Figure 5a and 5b). This observation could be explained by the difficulties the girl had in naming the shapes or in describing the place of the shape. Often (12 times) these deictic gestures were not accompanied with any verbal expression. For example, when the child wanted to use the trapezoid, she conveyed her idea stretching her hand and indicating with her pointing finger the trapezoid without speaking (line 29). The child produced deictic gestures also when she used verbal expressions such as, “this shape” and “here” (9 times, e.g., lines 2-4).

4.1.2. Types of gestures on paper

The child’s constructed representation with paper is shown in Figure 6. Two extracts of the talk between the child and the experimenter and their gestural production at the beginning and at the end of the activity on paper based on the video - recorded material are given next

At the beginning of the activity:

31 E: I would like you to choose the first shape that you want.

32 C: This (indicates the hexagon with her pointing finger).

33 E: This one? Nice. Do you remember its name? (….) Its name is hexagon. And, where do you want to put it?

34 C: (Shows with her pointing finger above the correct place, at the upper part of the figure).

35 E: Fine. I will put it here. Is it right here?

36 C: No.

37 E: What would you like to do?

38 C: You must move it down (she opens her palms to form a flat surface and moves them down).

39 E: Helen, you are amazing. I will turn it (makes a rotation using her pointing fingers). I am taking this tool and I am starting to turn it. Is it right here?

40 C: Nice, I will move it down. Is it right now?

41 E: Little, little (she points up with her finger).

42 C: You have to turn it again (makes a rotation with her pointing fingers, using both of them as moving points).

43 E: Little bit up? Is it right?

44 C: Yes.

45 E: Nice. Show me the next shape that you want to continue with.

46 C: With this (indicates the rhombus with her pointing finger).

47 E: With the rhombus, and where do you want to put it?

48 C: Here (points close to the correct place, down on the left side of the outline, with her finger).

49 E: Nice, I will put it here. Is it right here?

50 C: No. You must turn it a little bit here (moves her hands from right to left).

51 E: Here? Is this right?

52 C: Yes.

53 E: Wonderful. Let’s continue. Choose a shape.

54 C: (She indicates the trapezoid with her finger).

55 E: Do you remember its name? (…) Trapezoid.

56 C: Trapezoid.

57 E: Where do you want to place it?

58 C: Here (indicates the correct place with her pointing finger, on the bottom of the figure).

59 E: I have put it here. Is it right?

60 C: No.

61 E: What do I have to do?

62 C: You have to turn it (she makes a rotation with her pointing fingers using both of them as moving points).

At the end of the activity:

63 E: Choose a shape.

64 C: (She indicates the trapezoid with her pointing finger).

65 E: You chose the trapezoid again. I think you like this shape more than the other shapes. Where do you want to place it?

66 C: Here (indicates a correct place on the right side of the outline with her pointing finger).

67 E: Is it right here?

68 C: Yes but move it little bit here (she moves her right hand from the left to the right).

Although the second activity differed in the SCR in which it was conducted, the child used the same kind of gestures about the rotation and translation of shapes as in the first SCR. For example, when the child asked the researcher to “turn” the trapezoid, she produced the same iconic gesture that she used on the first type of SCR (made a rotation using her pointing fingers as moving points) (lines 72-73, Figure 7a). Such a congruence was identified also in the case of the horizontal translation. In order to apply a horizontal translation on a shape she produced a similar iconic gesture which was produced on the first SCR (line 59, Figure 7b), using either the wrong term “turn” at the beginning, or the correct term “move” later on (line 81). For the vertical shape translation (up and down), though, there was a difference in her words between the two SCRs. Although the child produced the same iconic gesture in the two SCRs, in the second SCR she used the appropriate term “move” from the beginning of the activity, while on the computer she did so only towards the end of the activity.

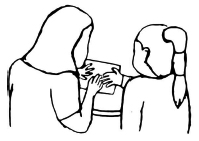
Similarly to the computer, on paper the child used deictic gestures with (e.g., lines 67-68) or without speech (e.g., lines 42-43) to show the shape she selected (e.g., line 63, Figure 8a) or the place of the shape on the composite figure (e.g., lines 78-79, Figure 8a).

4.2. Interrelations between child processes of geometrical figure apprehension and gesturing

In examining the second research question, we found that the child used different types of gestures when activating the perceptual or the operative apprehension of the geometrical figures in the shape configuration problem. In Table I some instances of the child’s verbal utterances and gestural production are analyzed to make apparent the connection between the child’s gesturing and processes of geometrical figure apprehension on the computer and on paper.

Table I shows that in both SCRs deictic gestures were likely to be produced by the child when she was in the process of recognizing a shape or the placement of a shape. Although the child was unable to name most of the shapes, her deictic gestures made it obvious that she was able to recognize all the shapes in the composite figure. The recognition of shapes in a perceived composite figure is an important component of perceptual apprehension. Thus, deictic gestures conveyed information drawing on the perceptual apprehension of shapes, and therefore served as a window for the child’s perceptual apprehension competences.

Additionally, in both SCRs, the child applied the place way of modifying a figure which is a basic component of the operative apprehension of geometrical figures. Specifically, when she selected the shape she thought would fit in a specific place, she was applying the rotation and sometimes the translation of the particular shape. This shape modification was expressed by the child through verbal expression and also, by iconic gestures which were used as a representational tool of these geometrical transformations. It is noteworthy that when the child used wrong verbal expressions (e.g., lines 23-24) for these transformations, gestures had a significant role to convey her ideas. Our microgenetic analysis of the child’s verbal and gestural production in both SCRs shows that at the first minutes of the activity in each SCR the child referred to two shape transformations (rotation and horizontal translation) using the same verbal expression, that is, “turn”, but two distinct iconic gestures (e.g., lines 9-10 and 23-24). Furthermore, with the wrong term “turn” for the horizontal translation she used both her hands to represent this transformation (see Figure 4b). By the end of the first and the second activity the child seemed to distinguish the two different geometrical transformations, rotation and horizontal translation, not only by gesturing but also by using two distinct words, “turn” (e.g., lines 72-73) and “move” (line 81). This progress was accompanied by another change: the shortening and simplification of the gesture about the transformation of horizontal translation, by using only one hand, at the last minutes of the activity with paper (Figure 9). For the vertical translation of shapes, such a mismatch between the child’s verbal utterances and gesture occurred only on the computer at the beginning of the activity, while the accompanying gesture did not change.

5. Discussion

5.1. Personal workspace of the child under study

Based on our results and the GWS for the solution of the shape configuration problem we can draw some conclusions about the personal GWS in which the child under study solved the particular task in the two SCRs and specifically about the three types of geneses. Our focus will be on the role of gestures within these geneses while the child dealt with the geometrical problem.

Within the visual genesis in both SCRs, the child’s visual work on the shape configuration and on the individual shapes involved the production 16 of gestures.

In fact, the child used deictic gestures to point to the recognized shapes that could fit and their location in the outline. Although the child could visually identify all the shapes in the outline, at both SCRs, she had difficulties with naming most of these shapes and, as a result the deictic gestures referring to the selected shapes were not always accompanied by the names of the shapes. This indicates that the deictic gestures had a significant role in conveying the child’s ideas about the selection of shapes, but they were also an indispensable component of her visual thinking.

Within the experimental genesis in both SCRs, while ‘manipulating verbally’ the geometrical shapes, the child produced relevant gestures which also played a significant role. In the context of the experimental genesis, though, the child did not use deictic, but iconic gestures which represented the shape transformations she proposed (rotation and translation).

Our results suggest that not only the verbal utterances of the child, but also her gestures had an essential role within the discursive genesis while solving the shape configuration problem. Particularly, the child used deictic gestures to show the location of a recognized shape in the outline without giving exact verbal explanations about its spatial position or relation with other shapes in the outline. She either did not use any verbal utterances or used the verbal expression “here” with the deictic gestures. This indicates that the deictic gestures were major components of the child’s spatial thinking and conveyed information that was not found in the child’s speech.

In the child’s discursive explanations about the shape transformations that were necessary for the shapes to fit in the outline, the iconic gestures also played a major role. This was more evident when wrong terms were used for a transformation by the child and the gesture conveyed the correct notion. At the beginning of each activity even though the child used the word “turn” to describe the horizontal translation of a shape, she produced an iconic gesture with the proper meaning (representing the displacement of a shape). By the end of the activity in each SCR a significant progress was identified. The child used an appropriate term for the shape horizontal translation and at the same time produced a congruent and more simplified and shortened gesture. The microlevel study of the child’s utterances and iconic gestures throughout the activity in both SCRs showed that the progress for the vertical translation occurred earlier relatively to the horizontal translation. An explanation is that the vertical shape translation is easier than the horizontal translation, as it involves the spatial concepts ‘up’ and ‘down’ which are less complex for young children than the concepts ‘left’ and ‘right’. Furthermore, the latter spatial concepts are used, not only as directions of moving horizontally a shape, but also as directions of turning a shape.

These findings about the child’s behavior in the context of discursive genesis indicated that both semiotic systems, words and iconic gestures, were necessary for the objectification of the notions of shape transformations by the child. Furthermore, they were essential for conveying the child’s ideas which are associated with operations of different complexity involved in the operative apprehension of geometrical shapes, and therefore, served as a window for identifying the child’s progress and difficulties.

In light of the above, deictic gestures’ production was associated to the recognition of geometrical shapes and their position in the outline and had a major role in the perceptual apprehension of shapes. Iconic gestures which were used to represent shape transformations had an important role in the operative apprehension of shapes. Both types of gestures were an integral part of the discursive reasoning for the solution of the problem, including the production of coherent instructions for combining the geometrical shapes to compose the larger composite figure and the implicit use of the notion that a shape remains the same in different positions and orientations.

Overall, these conclusions, on the one hand, indicate the multifunctional role of gestures in the child’s cognitive processes within the three fundamental geneses taking place in a relatively simple geometrical activity. On the other hand, these conclusions suggest that GWS could be a useful conceptual framework or tool to analyze the complex phenomenon of gestures in geometrical work.

5.2. Concluding remarks

The child in this case study was able to describe changes in the orientation and in the placement of geometrical shapes (e.g., trapeziod) in both SCRs, implying that she could recognize geometrical shapes in different positions other than the prototypical ones (e.g., horizontal base) (Levenson, Tirosh and Tsamir, 2011). From a Piagetian perspective, this could be a result of the gestural and verbal production of the child, with gestures often preceding the appropriate words. However, the child’s actions were enabled by a work space in which the geometrical activity took place (Kuzniak, 2012). From this broader perspective, the child’s understanding was accomplished through the alignment of the meaning of the representations in this work space and the meaning constructed by the child for these representations (Radford et al., 2005) through her verbal and gestural acts framed by the adult (researcher) and the context of the particular activity. This finding actually indicates that there is something to gain from the complex interplay between the geometrical figures, configurations and spatial transformations provided by the computer or on paper, and the verbal utterances and gestures produced by the child while using them. This semiotic coordination of culturally developed and personally developed resources (Radford et al., 2005) within a GWS may have helped the child to enter into a process of differentiating between critical and non - critical attributes (position or orientation) of shapes.

The SCR which the child interacted with in the geometrical activity was found to differentiate her gestural production. Although in both SCRs the child produced the same two types of gestures, iconic and deictic, on paper, the child produced a lower amount of iconic gestures than on the computer. This difference could be explained by the fact that the visual features of the applet on the computer, e.g., the image of the spin tool, and its clear dynamic character, e.g., the slow and step-by-step rotational function of the tool on shapes, encouraged the use of iconic gestures depicting spatial transformations. Considering the view that representational gestures are helpful when speakers have spatial images in mind (Kita, 2000), we can assume that the mathematical applet helped the child to produce these images in her mind and to be able to express them by gesturing. This inference is further supported by the fact that the child kept using the same types of iconic gestures also on paper. However, to be able to reach safer conclusions about the dynamics between the different SCRs in relation to children’s semiotic activity in a geometrical task, as well as the influence of these SCRs on children’s geometrical learning (e.g., lessening the impact of prototypes), the effects of reversing the order of the two SCRs needs to be considered. This could be addressed in a future study with a larger number of participants.

The above findings and conclusions, which were drawn on the micro - analysis of the data in this case study, and their connection to the GWS, can be considered as useful hints about young children’s embodied nature of thinking in relation to geometrical concepts. They could serve as a basis for continuing research about how gestures contribute to the investigation of the thinking of children in their early years and support their learning in geometry. Longitudinal observations of a larger number of kindergarten children, even younger children, including boys and girls, in shape configuration tasks of various levels of complexity should be carried out to give further insight into the role of gestures and their interaction with the SCR in geometrical development.

Referencias

Battista, M.T. (1999). The importance of spatial structuring in geometric reasoning. Teaching Children Mathematics, 6 (3), 170–177.

Brousseau, G. (1983): Etude de questions d’enseignement, un exemple: la géométrie. Séminaire de didactique des mathématiques et de l’informatique, (pp. 183–226). Grenoble: IMAG.

Clements, D. H., & Sarama, J. (2009). Learning and teaching early math: The learning trajectories approach. New York: Routledge.

Duval, R. (1995). Geometrical Pictures: Kinds of representation and specific processes. In R. Sutherland and J. Mason (Eds.), Exploiting mental imagery with computers in mathematical education (pp. 142–157). Berlin: Springer.

Duval, R. (1998). Geometry from a cognitive point of view. In C. Mammana and V. Villani (eds.), Perspectives on the Teaching of Geometry for the 21st century (pp. 37–51). Dordrecht: Kluwer Academic.

Ericsson, K. A., and Simon, H. A. (1980). Verbal reports as data. Psychological Review, 87 (3), 215–251.

Gallese, V., & Lakoff, G. (2005). The brain’s concepts: The role of the sensory - motor system in reason and language. Cognitive Neuropsychology, 22, 455–479.

Kim, M., Roth, W. M., and Thom, J. (2011). Children’s gestures and the embodied knowledge of geometry. International Journal of Science and Mathematics Education, 9, 207–238.

Kita, S. (2000). How representational gestures help speaking. In D. McNeill (Ed.), Language and gesture (pp. 162–185). Cambridge, UK: Cambridge University Press.

Kuzniak, A. (2009). Un essai sur la nature du travail géométrique en fin de la scolarité obligatoire en France. In A. Gagatsis, A. Kuzniak, E.Deliyianni, and L.Vivier (Eds), Cyprus and France Research in Mathematics Education (pp. 71–90). Lefkosia: University of Cyprus.

Kuzniak, A. (2012). Understanding the Nature of the Geometric Work Through its Development and its Transformations. Proceedings of the 12th International Congress on Mathematical Education. Seoul, Korea. Retrieved on November 4, 2012 from http://www.icme12.org/upload/submission/1922_F.pdf

Kuzniak, A. and Rauscher, J. C. (2011). How do teachers’ approaches to geometric work relate to geometry students’ learning difficulties? Educational Studies in Mathematics, 77 (1), 129–147.

Lavelli, M., Pantoja, A. P. F., Hsu, H., Messinger, D., & Fogel, A. (2005). Using microgenetic designs to study change processes. In D. M. Teti (Ed.), Handbook of research methods in developmental science (pp. 40–65). Malden, MA: Blackwell Publishing.

Levenson, E., Tirosh, D., & Tsamir, P. (2011). Preschool geometry: Theory, research and practical perspectives. Rotterdam: Sense Publishers.

McNeill, D. (1992). Hand and mind: What gestures reveal about thought. Chicago: The University of Chicago Press.

Nemirovsky, R., & Ferrara, F. (2009). Mathematical imagination and embodied cognition. Educational Studies in Mathematics, 70, 159–174.

Radford, L. (2003). Gestures, speech, and the sprouting of signs: A semiotic - cultural approach to students’ types of generalization. Mathematical Thinking and Learning, 5 (1), 37-70.

Radford, L. (2009). Why do gestures matter? Sensuous cognition and the palpability of mathematical meanings. Educational Studies in Mathematics, 70, 111-126.

Radford, L., Bardini, C., Sabena, C., Diallo, P., & Simbagoye, A. (2005). On embodiment, artifacts, and signs: a semiotic - cultural perspective on mathematical thinking. In Chick, H. L. & Vincent, J. L. (Eds.), Proceedings of the 29th Conference of the International Group for the Psychology of Mathematics Education, Vol. 4, pp. 113-120. Melbourne: PME.

Siegler, R. S. (1995). How does change occur: A microgenetic study of number conservation. Cognitive Psychology, 25, 225–73.