Dans Tanguay et Geeraerts (2012), nous proposons un cadre de travail en géométrie à travers lequel sont repensés les dialectiques empirisme - formalisme, inductif - déductif et le rôle du mesurage comme processus de validation. Il s’appuie sur près de cinq années de mise en œuvre, entre 2002 et 2007, dans des classes de sixième et cinquième où l’un des auteurs a été enseignant. Cette mise en œuvre ne s’insérait cependant pas dans un projet de recherche systématique appuyé d’un encadrement théorique adapté. Le présent article participe de l’élaboration progressive d’un tel encadrement, et doit être considéré comme un prolongement de l’article de 2012, dont certains éléments seront repris selon une perspective que l’éclairage des Espaces de Travail Mathématiques (ETM) infléchira quelque peu. Par ailleurs, des expérimentations plus systématiques sont amorcées et feront l’objet d’autres publications (voir par exemple les deux travaux de Tanguay, Geeraerts, Saboya, Venant, Guerrero & Morales, 2013 et Tanguay, Venant, Saboya & Geeraerts, 2013 abrégés par la suite Tanguay et al., 2013).

Reconnu d’abord par nous comme point de convergence des vues d’un praticien et d’un chercheur, ce cadre a été pensé comme un ensemble d’hypothèses, modes et pratiques de travail visant à assurer une transition plus harmonieuse entre la GI et la GII (Houdement & Kuzniak, 2006). Nous en avons donc parlé comme d’un paradigme, le paradigme du géomètre - physicien. On pourra alléguer que le terme paradigme est ici abusif : la « communauté scientifique » qui adopte et partage les convictions, savoirs et pratiques en cause (Kuhn, 1996) ne compterait que deux membres ?‼ Nous l’avons tout de même retenu d’une part, pour bien mettre en évidence le rôle d’articulation qu’a le cadre dans le passage entre deux paradigmes ; d’autre part, parce qu’il nous apparaît essentiel, pour des raisons que nous allons développer, d’impliquer toute la classe dans les choix, les problématisations et les motivations à la source du travail visé : la communauté en question, pour nous, c’est donc en fait la classe !

Parmi ces problématisations mises en avant pour la classe, il y a celle de la fiabilité de la mesure, du type et du degré de certitude auxquels elle donne accès. Quand les mesures sont données directement par un logiciel de géométrie dynamique comme Cabri ou GeoGebra, la question se complexifie parce que le rapport des élèves à de telles mesures, à leur exactitude et à leur précision, n’est évidemment pas le même que pour des mesures effectuées et lues sur une règle graduée ou un rapporteur. Entre autres, la majorité des élèves est spontanément persuadée qu’il ne saurait y avoir « erreur de mesure » avec ces logiciels. Comment, dès lors, éviter que l’utilisation que les élèves en font ne se substitue à la démonstration et ne provoquent « un glissement implicite et potentiel vers un Espace de Travail Géométrique (Houdement & Kuzniak, 2006) où l’expérience et les artefacts guident le travail » (Kuzniak, 2010, p. 79) ? Ces questions seront abordées en seconde moitié du présent article. Elles recoupent largement celles traitées par Dahan (2005) dans sa thèse. Celle-ci constitue une étude de grande ampleur que nous ne connaissions pas et que nous commençons à peine à « croiser » avec la nôtre.

1. Un référentiel théorique physiquement intégré à l’espace local

Dans Tanguay (2005, 2007), nous avons fait valoir que le passage de l’argumentation à la démonstration (Duval, 1991) nécessite des élèves une véritable « décentration » — au sens que Piaget (1997) donne à ce mot — par laquelle l’élève « reconsidère la primauté de ce qui est en jeu, la validité des enchaînements devant prendre le pas sur la vérité des propositions sans toutefois l’occulter… » (Tanguay & Geeraerts, 2012, p. 9). Ce « nouveau » point de vue relève d’un regard méta et ne sera possible, n’aura de sens pour les élèves que s’ils sont pleinement impliqués dans l’édification d’une théorie, dans la construction d’un réseau de résultats inter - reliés qui s’enchaînent dans la théorie de la même façon que les propositions s’enchaînent dans chaque démonstration : « on n’atteint pas pleinement l’idée de preuve en étudiant des preuves isolées » (Rouche, 1989, p. 9). Kuzniak (2010) met bien en évidence qu’en France, un travail sur des îlots déductifs, qu’il analyse comme relevant de la Géométrie II morcelée, est insuffisant pour empêcher que la géométrie du collège et du lycée ne glisse « subrepticement » vers la GI : « la preuve axiomatique […] est d’autant plus affaiblie que le référentiel théorique mis à disposition des élèves n’apparaît pas, même en filigrane » (Kuzniak, 2010, p. 87). Il ne fait pour nous aucun doute qu’un tel glissement est également observable dans la scolarité québécoise actuelle du secondaire (12 à 17 ans) : voir par exemple Braconne - Michoux (2013)

Dans le cadre que nous proposons, une partie substantielle et bien identifiée du référentiel théorique est construite par la classe — nous verrons plus loin selon quelle perspective — et donne lieu à un outil, le classeur, intégré à l’espace local. Selon le modèle théorique des ETM en deux plans (Figure 1 dans Kuzniak & Richard, 2014), le classeur peut être vu comme un artefact dans le plan épistémologique, artefact tant au sens usuel d’objet physique fabriqué (par l’homme) qu’au sens plus élargi d’artefact symbolique (Rabardel, 1995), puisqu’il contient les définitions, propriétés et théorèmes sur lesquels l’élève s’appuiera pour élaborer des preuves. Nous suggérons en effet de donner aux énoncés du référentiel la forme d’un répertoire de définitions et de « règles » — nous discuterons plus loin des différents statuts à donner à ces règles — dont chacune fait l’objet d’une fiche dans le classeur. Le contenu de chaque fiche est élaboré et décidé par le groupe classe mais chaque élève en transcrit sa copie qu’il insère dans son propre classeur. Le format des fiches (24 cm × 16 cm) et par conséquent du classeur est choisi pour que l’élève puisse l’ouvrir dans le haut du bureau tout en laissant libre un espace de travail — au sens bien physique et concret cette fois —, celui où il mènera les constructions ou tracés à l’étude, examinera et codera des figures déjà tracées, organisera les fiches sorties du classeur quand elles sont susceptibles d’intervenir comme règles d’inférence (Duval, 1991) dans une démonstration en chantier, etc.

En effet, quand le travail vise une démonstration spécifique, on désamorce une des principales sources de déconvenue en faisant de l’ensemble des fiches le corpus (explicitement identifié) des résultats disponibles pour démontrer. Le contrat est alors clair sur ce qu’on « a le droit d’utiliser », et permet par ailleurs à l’enseignant de varier les scénarios : laisser libre accès au classeur, imposer un sous - ensemble de fiches suffisantes, etc. De leur côté les élèves, à l’issue d’une phase heuristique liée à une conjecture, peuvent ressentir le besoin d’utiliser des règles qui ne figurent pas encore dans le classeur et les proposer à la classe comme cibles de travail.

2. Une articulation, à plusieurs niveaux, entre les registres discursif discursif et figural

Dans les fiches, chaque règle et chaque définition est énoncée discursivement et représentée figuralement. Les règles sont illustrées en tant qu’implication, l’antécédent et le conséquent étant chacun représenté par une figure - clé (Kerboeuf & Houdebine, 2005). Incidemment, les équivalences qui ne sont pas retenues comme définitions donnent systématiquement lieu à deux fiches, une pour chaque implication. Pour plus de détails, notamment sur les fiches - définitions, on pourra consulter Tanguay et Geeraerts (2012).

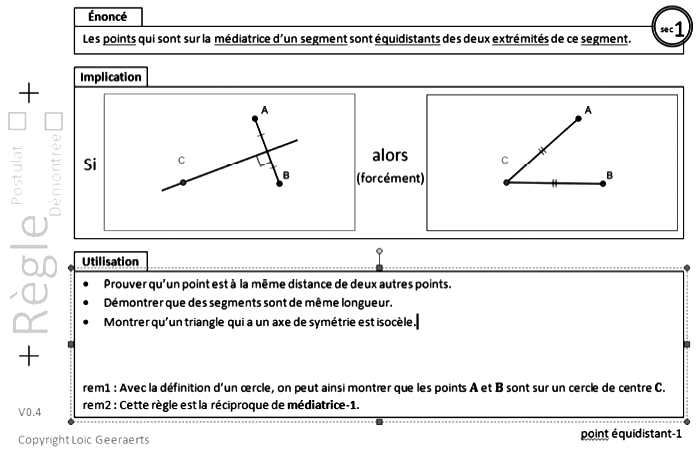
Il y a là plus que l’articulation entre les registres figural et discursif (Duval, 1993). Il s’agit en effet d’un aspect central de l’étude de la géométrie, constituant à la fois l’une de ses richesses mais aussi l’une de ses pierres d’achoppement : articuler le sensible et l’intelligible, apprendre « à utiliser ses perceptions et son intuition pour guider les raisonnements plutôt que de leur faire obstacle, […] travailler progressivement à distinguer ce qui doit relever des uns et des autres » (Geeraerts & Tanguay, 2012, p. 25). Les travaux de Duval (1991, 1995) ont mis en évidence que la structure par enchaînement d’inférences des démonstrations n’est ni naturellement, ni même facilement comprise des élèves, et que les raisonnements qu’ils mettent en oeuvre spontanément, visant à convaincre et obéissant à des critères de pertinence, « […] ne permettent pas d’entrer dans le fonctionnement cognitif de la démonstration qui obéit, elle, à des critères de validité et cherche à prouver » (Duval, 1995, p. 213). Dans la foulée de ces travaux, des dispositifs et outils d’enseignement — incluant des tutoriels — relativement pointus sont proposés, où le travail d’organisation des propositions occupe l’avant - plan : Duval (1991), Tanguay (2005, 2007), Richard et al. (2011), Guerrero Magaña (2011).

Mais l’analyse du travail (représentatif) d’un trio d’élèves cherchant à reconstituer une démonstration via un déductogramme (Tanguay, 2007) montre bien que l’élève qui « performe » vraiment et qui, de fait, trouve la solution pour son équipe, est celui qui fait constamment le lien entre les propositions manipulées (via des petits cartons) et la figure, allant même jusqu’à tracer à nouveau la figure pour lui-même. Il s’agit typiquement de ces allers et retours dialectiques entre sémantique et syntaxe, que Barrier, Durand - Guerrier & Blossier (2009) identifient et décrivent comme étant au coeur même du processus d’élaboration des démonstrations.

Si l’on cherche à analyser un tel travail à l’aide du modèle en deux plans de l’ETM (Figure 1, in Kuzniak & Richard, 2014), on voit bien qu’il engage, dans le plan épistémologique, à la fois des énoncés qui relèvent directement du référentiel « les règles d’inférence » (Duval, 1991), des figures tracées dans l’espace local, et d’autres énoncés — les « propositions d’entrée » pour chaque inférence — qui sont particularisés à ces figures et ne proviennent donc pas directement du référentiel. Les figures constituent des representamen (ou signifiants) mais aussi des représentants (génériques) d’objets théoriques : une figure (particulière), par exemple celle constituée d’un segment XY et de sa médiatrice passant par Z, doit pouvoir représenter toutes les configurations (soumises aux mêmes hypothèses) des objets théoriques segment et médiatrice. Ce sont les définitions et propriétés de ces objets qui fournissent les propositions d’entrée des inférences dans la démonstration : par exemple la proposition « les segments [XZ] et [YZ] sont de même mesure », découlant de la règle « les points de la médiatrice d’un segment sont équidistants des extrémités de ce segment ». Mais les énoncés du référentiel doivent pour cela avoir été projetés dans la figure, selon une direction qui dans le plan épistémologique va du référentiel vers les representamen, et dont la parallèle dans le plan cognitif pourrait être désignée par l’instanciation : la démarche intellectuelle consistant à particulariser les définitions, relations et propriétés à la figure à partir de laquelle le sujet travaille. Sans l’instanciation, le contrôle sémantique est quasi - impossible. Mais elle peut par ailleurs s’ériger en obstacle quand l’élève n’arrive pas ensuite à remonter dans la direction inverse et à comprendre en quoi son travail (de démonstration) engendre des énoncés généraux, universels (cf. par exemple Chazan, 1993).

En géométrie, dans la phase de recherche d’une preuve donnée, ce contrôl sémantique de l’enchaînement déductif se fait entre autres à travers le codage de la figure, à condition que l’élève garde une trace — par la mémoire, par un jeu de couleurs, en faisant plusieurs copies de la figure… — de la sériation des propriétés déduites (Tanguay & Geeraerts, 2012, p. 9) et codées à mesure : il ne s’agit pas seulement de savoir par exemple que deux segments sont isométriques dans telle figure pour construire la preuve visée, il faut savoir à partir d’où dans la sériation on a pu tirer cette conclusion et comment. Ainsi, le codage tient certes d’une forme de visualisation mais c’est une visualisation qui doit en quelque sorte être décomposée, segmentée en différents « moments » selon une ligne de temps (artificiellement) générée, dont l’élève doit savoir retrouver la trace dans le discours déductif quand il cherche à organiser des enchaînements valides. Le processus sollicite donc en ce sens une coordination subtile et complexe entre les registres discursif et figural puisqu’en même temps, les propriétés codées sont puisées dans le référentiel théorique, dans le corpus de définitions et théorèmes d’où sont issues les règles d’inférence. En outre, le codage doit parfois se faire en parallèle avec un travail de construction, quand la figure n’est pas initialement donnée ou quand des éléments doivent y être ajoutés. Ces considérations montrent la complexité de l’activité de démonstration en géométrie. Il s’agit bien d’une démarche relevant principalement de la validation, mais qu’on peut difficilement circonscrire au plan vertical suggéré par la Figure 10 de Coutat et Richard (2011), repris comme plan de la « Démarche de validation » dans la Figure 4 de Kuzniak et Richard (2014). On mesure bien aussi la difficulté qu’il y a à susciter chez les élèves ces coordinations, et la complexité de ce que peut être un dispositif didactique efficace pour le faire.

Nous faisons l’hypothèse, en grande partie corroborée par nos expériences d’enseignement, que les figures - clés représentant les règles figuralement dans les fiches favorisent le contrôle sémantique de l’organisation déductive, entre autres parce que la disposition gauche - droite, antécédent - conséquent, des deux figures codées suggère la sériation des propositions. Si les deux registres (figural et discursif) sont coordonnés au niveau local de chaque règle, la possibilité de manipuler physiquement les fiches sur l’espace (réel) de travail permet aussi un contrôle visuel et kinesthésique de l’organisation syntaxique au niveau global. Ce contrôle peut être poussé plus loin encore avec la construction de déductogrammes selon le format spécifiquement adapté que nous proposons (Tanguay & Geeraerts, 2012), sur lequel cependant nous ne reviendrons pas ici.

Le fait que tel ou tel énoncé soit une règle plutôt qu’une définition relève bien sûr d’un choix : on pourrait par exemple décider de définir la médiatrice comme lieu des points équidistants des extrémités du segment, auquel cas la règle à établir ensuite serait celle selon laquelle la médiatrice coupe le segment à angle droit, en son milieu. C’est bien en ce sens que nous avons insisté, en §1, sur l’aspect suivant : de la même façon qu’il y a sériation des propositions au niveau local de chaque démonstration, il y a sériation des énoncés au niveau global de la théorie, comme l’étymologie de ce mot (θεωρια, procession) devrait nous le rappeler. Il nous apparaît crucial d’éveiller les élèves à cette correspondance car c’est en partie à travers elle qu’ils construisent le sens à donner à l’activité de démonstration. Il s’agit donc d’impliquer pleinement la classe dans l’édification de la théorie, dans les choix à faire justement et dans l’organisation qu’elle doit gérer en fonction de ces choix. Il s’agit aussi de les sensibiliser à la beauté architectonique des mathématiques.

3. Des règles comme des lois de la physique

Mais comment concilier cette édification théorique avec l’exploration et l’expérimentation par mesurage ? Comment initier la motivation à démontrer sans que les élèves « ne voient dans la démarche de raisonnement formel, en particulier dans la démonstration, qu’une pratique imposée plus ou moins gratuitement par les professeurs, mais sans utilité réelle » (Pluvinage, 1989, p. 6) ? Quoi faire pour convaincre l’élève de 12 ou 13 ans, à qui l’on continue de demander constructions et mesures aux instruments, que les démarches déductives sur lesquelles on le fait travailler ensuite ont du sens, et apportent une certitude qui est d’un autre ordre que celle à laquelle le mesurage lui a donné accès ? C’est ici que le « physicien » intervient.

Notre approche peut certainement être apparentée à celle du « débat scientifique » de M. Legrand et du groupe de recherche de Grenoble attaché à ce thème : il s’agit d’entrer « dans un processus de dénaturalisation ¹ et d’institutionnalisation systématique [des] objets de savoirs indispensables […] à la compréhension du jeu qui se joue dans les institutions scientifiques » (Legrand, 1988, p. 371). La classe est vue comme une communauté de chercheurs, l’abord de la géométrie y est analogue à celui qu’on initierait dans un laboratoire de physique, et la question de la fiabilité de la mesure et de l’empirisme y est ouvertement et systématiquement problématisée, discutée. On cherche à mettre en place le contrat (didactique) suivant : les résultats du cours de géométrie doivent, avant d’être intégrés au classeur (et donc d’être invoqués dans une preuve), faire l’objet soit d’une démonstration, soit d’une vérification expérimentale. Quand celle-ci est faite aux instruments — règle graduée, équerre, rapporteur —, les imprécisions et les erreurs de mesure sont utilisées pour mettre en évidence le caractère hypothétique ² du résultat. Selon notre perspective, résolument vigotskienne au regard du rôle qu’y l’enseignant (Bartolini Bussi & Mariotti, 2002), celui-ci doit faire la promotion active de l’état d’esprit qui préside : exiger par exemple que le signe d’approximation « ≈ » soit utilisé, plutôt que l’égalité, pour rendre compte de toute mesure obtenue aux instruments ; veiller le cas échéant à rendre cette idée explicite dans les formulations (« les deux segments semblent isométriques ») ; prévoir des activités où résultats expérimentaux et résultats théoriques sont confrontés, par exemple l’admirable séquence proposée par Jahnke (2007, §6). Quand la vérification expérimentale est faite avec des logiciels de géométrie dynamique, le problème se corse : nous en discuterons en §4.

Pour obtenir un engagement optimal des élèves, nous suggérons de travailler sur des résultats où l’intuition est en défaut — la somme des angles du triangle peut constituer l’un des premiers de ces résultats — afin que la démonstration apparaisse autant comme levier pour lever l’incertitude amenée par une éventuelle vérification empirique, que comme moyen pour expliquer (Hanna, 1995). Les résultats plus intuitifs qui émergent alors comme règles d’inférence nécessaires à la démonstration, s’ils ne font pas déjà l’objet d’une fiche, sont d’abord énoncés par la classe, puis proposés pour vérification expérimentale. Ce sont les « règles - postulats » (voir Fig. 1, à gauche), qu’on ne démontre pas (pour l’instant). À plus longue échéance, l’enseignant a le rôle de repérer les règles - postulats que le développement de la théorie a rendu accessible à la démonstration. Quand par la suite elle est de fait démontrée, la règle change de statut et la case « démontrée » dans la marge de gauche de la fiche est cochée. Le groupe classe réalise ainsi progressivement l’articulation des îlots en réseau, ce à quoi contribue également le cumul des règles dans le classeur.

4. Les logiciels de géométrie dynamique, comme outils expérimentaux de vérification

L’usage le plus standard des Logiciels de Géométrie Dynamique (LGD) proposé par la littérature consiste à construire une figure, l’investiguer par déformation (dragging) et conjecturer telle ou telle propriété. Du point de vue de l’enseignement, on est alors confronté au problème que pour les élèves, il devient inutile de démontrer les propriétés conjecturées : le logiciel est si précis que ce qu’il laisse à voir est forcément vrai (Kuzniak, 2010, p. 86). Cela tient à plusieurs raisons :

1. 1. Graphiquement, la précision des tracés vectoriels ³ (au sens informatique) alliée à l’utilisation du zoom procure un sentiment de perfection (par exemple, quand trois droites sont concourantes).
2. 2. Numériquement, pour les mesures, le nombre de décimales auquel l’élève a accès peut lui donner l’impression que tous les nombres sont manipulés exactement par l’ordinateur.
3. 3. Généralement, le sentiment plus ou moins conscient de la supériorité de la machine sur l’homme (et en particulier sur l’enseignant…)

Dans notre cadre, quand le résultat est une règle - postulat que la classe se contente de vérifier expérimentalement, c’est son caractère hypothétique qui est compromis par la trop grande fiabilité allouée par les élèves au LGD. Quand il s’agit d’une conjecture ⁴ dont la démonstration est visée, c’est la pertinence même de cette démonstration qui sera remise en cause. Penchonsnous plus spécifiquement sur ce problème du point de vue de l’exactitude des mesures données par GeoGebra.

Exemple 1

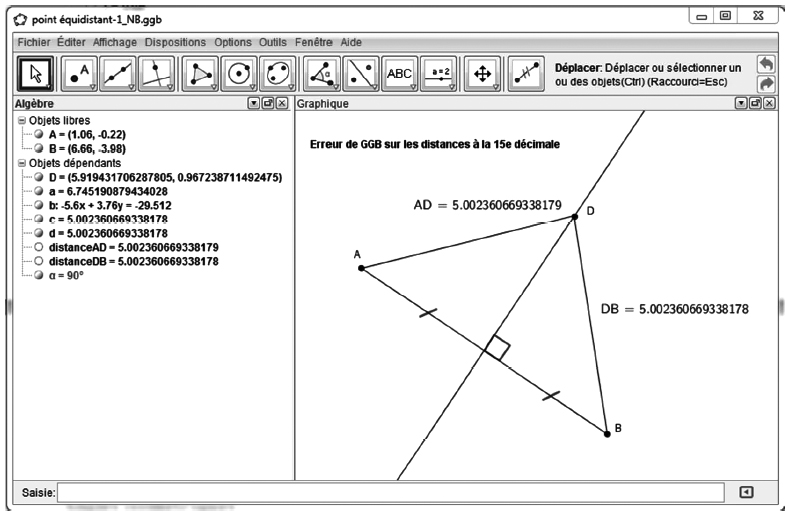
La démonstration de la règle « point équidistant - 1 » (Fig. 1) n’est pas élémentaire, et nécessite un arsenal théorique relativement important : propriétés de la symétrie orthogonale, Théorème de Pythagore ou critères d’isométrie des triangles. Mais elle est par ailleurs intuitivement presque évidente. Supposons que la classe veuille en faire une règle - postulat en la vérifiant expérimentalement (cette règle - postulat intervient par exemple dans la séquence proposée par Geeraerts & Tanguay, §3). Dans la construction GeoGebra (GGB, version 4.0.38.0) suivante, le point D est placé sur la médiatrice de [AB]. Ayant fait afficher les distances entre A et D, puis entre D et B, avec les deux décimales données par défaut, les élèves concluent à l’isométrie de [AD] et [DB], quelle que soit la position de D. On s’aperçoit par contre que pour certaines positions de D, ces distances diffèrent à la 15^e décimale. On peut donc se servir de ce dysfonctionnement pour faire douter les élèves et discuter avec eux de la réelle isométrie de [AD] et [DB]. Or, GGB fait apparaître ici un autre dysfonctionnement : la mesure de [AD] n’est pas exactement égale à la distance entre A et D. La mesure de [AD] est le nombre c dans la fenêtre « Algèbre », apparu automatiquement lors de la création du segment. La distance de A à B a été obtenue avec le bouton « Distance ou Longueur » en cliquant successivement sur les points A et B.

Les arrondis des mesures de [AD] et [DB] donnés par GGB sont les mêmes, alors que les arrondis des distances diffèrent. Il s’agit de bien faire valoir auprès des élèves que tous les nombres donnés par GGB sont des arrondis et que par conséquent, des mesures affichées égales ne permettent pas en théorie de conclure à l’isométrie. La remarque s’applique d’ailleurs plus généralement aux logiciels de géométrie dynamique, aux calculatrices et aux tableurs. Par contre, la contraposée de [ k = l ⇒ arrondi _n (k) = arrondi _n (l) ] devrait, en toute rigueur, amener à conclure à la non - isométrie quand les arrondis, à la n-ième décimale pour un n fixé, sont différents.

Cette démarche critique peut conduire la classe à s’interroger sur la façon dont les nombres sont stockés dans le logiciel, voire dans un ordinateur : sontils représentés sous forme décimale ? Si oui, combien de décimales sont prises en compte ? Que se passe-t-il avec les nombres rationnels d’écriture décimale infinie ? Qu’en est-il d’un irrationnel comme π ? Ces questions créent des liens entre la géométrie et l’arithmétique (voir Tanguay et al., 2013) mais surtout, permettent de développer un esprit critique face aux informations données par les LGD. Nous pensons qu’une gestion appropriée de la situation par l’enseignant permet de préserver, vis-à-vis des élèves, le caractère hypothétique du résultat.

Exemple 2

Supposons maintenant que la classe se questionne sur la somme des mesures des angles intérieurs des triangles. Dans une approche sur papier aux instruments « classiques », selon nos propres expériences d’enseignement, la dispersion des différentes sommes trouvées par les élèves est souvent trop importante pour qu’ils pensent à conjecturer la valeur 180. Par contre, l’utilisation de GGB fait apparaître clairement une somme constante de 180°, ainsi les élèves énoncent sans hésiter la conjecture. Comment, ici, aborder la motivation à la démonstration ? Ci-dessous, les figures obtenues en faisant afficher, par GGB, les mesures de chacun des côtés d’un triangle à 10 décimales, puis à 15. On constate, par simple inspection de la dernière décimale de chaque nombre, que la somme des mesures affichées ne donne pas 180 ni dans un cas ni dans l’autre.

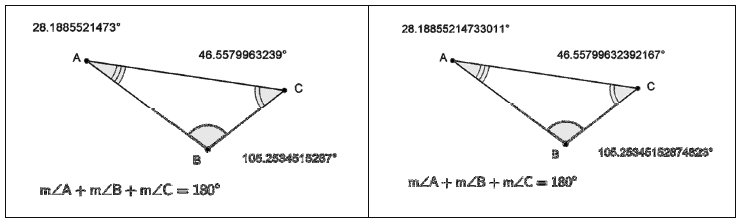
Quand l’enseignant ou les élèves débrouillards font calculer la somme par GGB via le champ de saisie (en bas de la fenêtre), comme c’est fait dans le bas des deux affichages ci-dessus, un nouveau problème se pose : le logiciel donne invariablement 180 quel que soit le nombre de décimales demandées. Cela force l’enseignant à des discussions pointues : GGB ne calcule pas la somme à partir des arrondis affichés mais se sert des arrondis qu’il conserve en mémoire grâce à sa représentation interne des nombres, qui y ont vraisemblablement beaucoup plus de décimales. Le déroulement d’une telle leçon se sera alors trouvé fortement influencé par le fonctionnement du logiciel et aura nécessité, comme outil d’enseignement, une « instrumentation » importante (Vérillon & Rabardel, 1995). Mais un enseignant pourrait alors évaluer son enseignement comme détourné de son objet premier, la géométrie, au profit d’un enseignement de GeoGebra ! Une alternative possible, relevant de « l’instrumentalisation » cette fois, est de préparer un fichier GGB dans lequel l’enseignant a forcé le logiciel à calculer la somme des arrondis affichés afin qu’elle ne soit plus constamment égale à 180°.

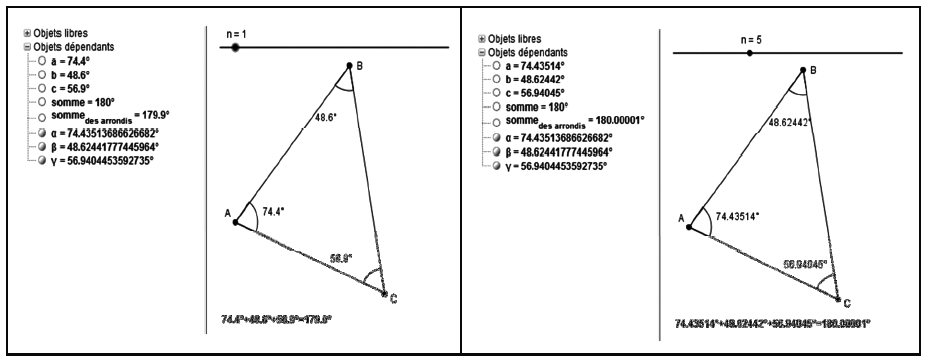
Pour arrondir la mesure α d’un angle donné, il suffit d’utiliser la fonction d’arrondissement à l’unité et de faire une translation sur les chiffres de la manière suivante : a = round (10^n*α) / 10^n, avec n le nombre de décimales voulues. Ainsi, il est possible d’additionner les arrondis affichés plutôt que ceux utilisés nativement par GGB. L’avantage d’un tel fichier, c’est qu’il donne lieu à des approximations de 180° qui ne restent pas constamment égales à 180, et que le besoin de démontrer reste alors vivant pour bon nombre d’élèves. De telles trajectoires d’enseignement devront bien sûr être ajustées en fonction du logiciel utilisé en classe. On trouvera des « équivoques » analogues avec le logiciel Cabri - Géomètre dans Dahan (2005, ch. 7, §4). Un logiciel comme CaRMetal, aux différences plus marquées avec GeoGebra ou Cabri, demandera à l’enseignant de repenser ses planifications en conséquence.

5. Conclusion

Sans négliger les fonctions usuelles qu’on prête aux LGD — outils de construction, avec l’opposition maintenant classique entre dessin et figure (par exemple Parzysz, 1988) ; outils d’exploration, permettant de repérer et énoncer des conjectures — ceux-ci peuvent être mis à profit pour des vérifications expérimentales donnant accès à des règles - postulats dont le caractère intuitif, le caractère « d’évidence » (Rouche, 1989) n’est pas propice à motiver des démonstrations. Seulement voilà, ce caractère d’évidence, l’enseignant ne veut pas le laisser dans les limbes, il veut en faire, tout comme le résultat luimême, l’objet d’une discussion, d’une problématisation. En effet, en mettant en évidence certaines défaillances ou imprécisions des LGD, il est encore possible de garder vivant l’enjeu de vérité (Grenier & Payan, 1998) lié à chaque énoncé, que celui-ci soit une conjecture ou une règle - postulat. Les discussions de classe qui en résultent, coordonnées au travail sur les fiches — notamment la décision à prendre en classe sur laquelle des deux cases à cocher à gauche de la ficherègle, voir la Figure 1 — augmente par suite le poids de l’institutionnalisation des énoncés et la signification des démonstrations où ceux-ci interviennent.

Le rapport à l’axiomatisation s’en trouve lui aussi changé, la « minimalité » du nombre des règles - postulats n’est plus un enjeu majeur, les processus impliqués sont intégrés à la construction de « théories locales », ayant recours à des « hypothèses » au sens de Jahnke, c’est-à-dire à des axiomes — nos règlespostulats — « qui ne sont pas plus des révélations d’êtres supérieurs que des expressions d’idées éternelles, mais simplement des constructions humaines » (Jahnke, 2010, p. 31, notre traduction). On cherche ensuite à connecter ces théories locales en réseau — l’enseignant a alors un rôle crucial par rapport aux tâches qu’il propose à la classe —, dans une démarche qui rapproche la géométrie des sciences expérimentales, avec des développements déductifs moins complexes que ceux de la géométrie euclidienne et par conséquent, des démonstrations dont on peut mieux contrôler, du point de vue de l’enseignement, la difficulté, l’accessibilité et la finalité.

Le cadre (ou paradigme !) du géomètre - physicien nécessite encore bien sûr réflexions et recherche, tant empirique que théorique. Parmi les questions à approfondir : celle de la technologie utilisée par les LGD du point de vue graphique, notamment sur l’abord des problèmes (et théorèmes) d’incidence ; la coordination du travail aux (bons vieux) instruments usuels avec le travail aux LGD ; que devient l’espace de travail lors des séances informatisées, etc.

Les références

Barrier, T., Durand - Guerrier, V. & Blossier, T. (2009). Semantic and Game - Theoretical Insight into Argumentation and Proof. In F. L. Lin, F. J. Hsieh, G. Hanna & M. de Villiers (eds), ICMI Study 19 Conference Proceedings, 1, pp. 77-82.

Bartolini Bussi, M. & Mariotti, M. A. (2002). Semiotic Mediation in the Mathematics Classroom: Artifacts and Signs after a Vygotskian Perspective. In L. D. English (ed.), Handbook of International Research in Mathematics Education, 2nd edition, pp. 746-783. NY & Abingdon, Royaume Uni : Routledge.

Braconne - Michoux, A. (2013). Quel espace de travail géométrique pour les élèves au Québec ? Pour les futurs enseignants ? In A. Kuzniak & P. R. Richard (eds), Actes du 3e symposium Espaces de travail mathématique (ETM3), Université de Montréal.

Chazan, D. (1993). High School Geometry Students’ Justification for their Views of empirical Evidence and mathematical Proof. Educational Studies in Mathematics, 24, pp. 359-387.

Coutat, S. & Richard, P. R. (2011). Les figures dynamiques dans un espace de travail mathématique pour l’apprentissage des propriétés géométriques. Annales de didactique et de sciences cognitives, 16, pp. 97-126.

Dahan, J. J. (2005). La démarche de découverte expérimentalement médiée par Cabri - Géomètre en mathématiques. Un essai de formalisation à partir de l’analyse de démarches de résolutions de problèmes de boîtes noires (Thèse de doctorat). Université Joseph Fourier, Grenoble, France. Repéré à : http://tel.archives-ouvertes.fr/docs/00/35/61/07/PDF/these_jjdahan1.pdf

Duval, R. (1991). Structure du raisonnement déductif et apprentissage de la démonstration. Educational studies in Mathematics, 22, pp. 233-261.

Duval, R. (1993). Registres de représentation sémiotique et fonctionnement cognitif de la pensée. Annales de Didactique et de Sciences Cognitives, 5, pp. 37-65.

Duval, R. (1995). Sémiosis et pensée humaine. Exploration, recherches en sciences de l’éducation. Berne, Suisse : Peter Lang.

Geeraerts, L. & Tanguay, D. (2012). GeoGebra comme outil d’exploration, d’expérimentation et de représentation des démonstrations, pour construire une théorie avec les élèves. Envol, revue du Groupe des responsables de mathématiques au secondaire (GRMS) du Québec, 1 (160), pp. 25-31 & 2 (161), pp. 45-48.

Grenier, D. & Payan, C. (1998). Spécificités de la preuve et de la modélisation en mathématiques discrètes. Recherches en didactiques des mathématiques, 18 (1), pp. 59-99.

Guerrero Magaña, L. (2011). El aprendizaje de la demostración a través de su estructura: una experiencia con estudiantes de bachillerato. In F. Hitt et C. Cortés, Formation à la recherche en didactique des mathématiques, pp. 251-256. Montréal, Québec : Éditions Loze - Dion.

Hanna, G. (1995). Challenges to the Importance of Proof. For the Learning of Mathematics, 15 (3), pp. 42-49.

Houdement, C. & Kuzniak, A. (2006). Paradigmes géométriques et enseignement de la géométrie. Annales de didactique et de sciences cognitives, 11, pp. 175-193.

Jahnke, H. N. (2007). Proofs and hypotheses. Zentralblatt für Didaktik der Mathematik, 39 (1-2), pp. 79-86.

Jahnke, H. N. (2010). The Conjoint Origin of Proof and Theoretical Physics. In G. Hanna, H. N. Jahnke & H. Pulte (eds), Explanation and Proof in Mathematics, Philosophical and Educational Perspectives. Springer, New - York.

Kerboeuf, M. P. & Houdebine, J. (2005). Les figures - clés : une idée pour l’apprentissage de la démonstration en Quatrième. Repères IREM, 59, pp. 83-103.

Kuhn, T. S. (1996) The Structure of Scientific Revolutions. 3rd edition. Chicago, Etats - Unis: The University of Chicago Press.

Kuzniak, A. (2010). Un essai sur la nature du travail géométrique en fin de la scolarité obligatoire en France. Annales de Didactique et de Sciences Cognitives, 15, pp. 75-96. Proceedings of the First French - Cypriot Conference of Mathematics Education, University of Cyprus, pp. 71-89.

Kuzniak, A. & Richard, P. R. (2014). Espaces de Travail Mathématiques. Points de vue et perspectives. Revista Latinoamericana de Investigación en Matemática Educativa, 17 (Número Especial TOMO I), pp. 29-39.

Legrand, M. (1988). Rationalité et démonstration mathématiques, le rapport de la classe à une communauté scientifique. Recherches en didactique des mathématiques, 9 (3), pp. 365-406.

Parzysz, B. (1988). «Knowing» vs «Seeing». Problems of the Plane Representation of Space Geometry Figures. Educational Studies in Mathematics, 19, pp. 79-92

Piaget, J. (1997). Commentaire sur les remarques critiques de Vygotski concernant Le langage et la pensée chez l’enfant et Le jugement et le raisonnement chez l’enfant. In Vygotski, L. (1997) Pensée & langage, 3e édition. Paris, France : La Dispute.

Pluvinage, F. (1989). Aspects multidimensionnels du raisonnement en géométrie. Annales de didactique et de sciences cognitives, 2, pp. 5-24.

Rabardel, P. (1995). Les hommes et les technologies, approche cognitive des instruments contemporains. Paris : Armand Colin.

Richard, P. R., Fortuny, J. M., Gagnon, M., Leduc, N., Puertas, E. & Tessier - Baillargeon, M. (2011). Theoretical Fundaments for an Intelligent Tutorial System Towards the Learning of Geometry at a High School Level. ZDM, Zentralblatt für Didaktik der Mathematik, 43 (4), pp. 425-439.

Rouche, N. (1989). Prouver : amener à l’évidence ou contrôler des implications ? La démonstration mathématique dans l’histoire. Colloque Inter - Irem Épistémologie et histoire des mathématiques, pp. 8-38. Besançon, France.

Tanguay, D. (2005). Apprentissage de la démonstration et graphes orientés. Annales de didactique et de sciences cognitives, 10, pp. 55-93.

Tanguay, D. (2007). Learning Proof: from Truth towards Validity. Proceedings of the Xth Conference on Research in Undergraduate Mathematics Education (RUME), San Diego State University, San Diego, Etats - Unis. Repéré à http://www.rume.org/crume2007/eproc.html

Tanguay, D. & Geeraerts, L. (2012). D’une géométrie du perceptible à une géométrie déductive : à la recherche du paradigme manquant. Petit x, 88, pp. 5-24.

Tanguay, D., Geeraerts, L., Saboya, M., Venant, F., Guerrero, L. & Morales, C. (2013). An activity entailing exactness and approximation of angle measurement in a DGS. Proceedings of the Eight Congress of European Research in Mathematics Education (CERME 8). Antalya, Turquie.

Tanguay, D., Venant, F., Saboya, M. & Geeraerts, L. (2013). An activity involving geometry, arithmetic and numerical representations. I Congreso de Educación Matemática de América Central y de El Caribe (I CEMACYC), Santo Domingo, République dominicaine.

Vérillon, P. & Rabardel, P. (1995). Cognition and Artefacts : A contribution to the study of thought in relation to instrumented activity. European Journal of Psychology of Education, 10 (1), pp. 77-101.

Notes

1 … au sens où selon Legrand, la communauté scientifique (et son double scolaire, les enseignants de science) a hégémoniquement stabilisé et cristallisé — Legrand dit ici « naturalisé », un emprunt à Chevallard — les savoirs et démarches constitutifs de la rationalité scientifique, au point où ceux-ci n’apparaissent plus aux membres (aux enseignants) comme objets de savoir (à enseigner), ces derniers étant par conséquent incapables de reconnaître tout autre forme de rationalité, notamment la rationalité « quotidienne » des élèves. Pour les faire réapparaître comme objets de savoir, il faut défaire cette « naturalisation ».

2 … au sens que les sciences expérimentales donnent à ce mot (cf. Jahnke, 2007 ; Tanguay & Geeraerts, 2012, note 8, bas de la page 12). Pour une discussion approfondie sur les sens qu’ont pu avoir les mots « hypothèses », « axiomes » et « postulats » chez les Grecs pré - socratiques, voir Jahnke (2010). Son argumentation met sur la piste d’une conception de ces termes, chez ces anciens Grecs, qui supposerait une approche hypothéticodéductive de la géométrie analogue à celle qui est usitée en physique.

3 Un tracé n’est pas produit à l’aide d’une matrice de pixels mais avec des fonctions que le logiciel traduit dynamiquement à l’écran. Ainsi, l’effet de pixellisation qui apparaissait à partir d’un certain niveau de zoom disparaît au profit d’une image toujours nette et dont les lignes, avec les LGD, gardent de surcroît toujours la même épaisseur.

4 Au regard de leur statut logique, nous ne faisons pas de différence entre postulat et conjecture. Nous parlons de conjecture quand il s’agit d’un énoncé qui est l’objet premier du travail en cours et dont on envisage la démonstration. Le postulat est quant à lui un outil qu’on se permet d’utiliser parce que sa valeur de vérité a un caractère d’évidence : les postulats correspondent donc aux axiomes de la GII, à cette nuance près que leur caractère hypothétique est ici pleinement assumé par la classe. De notre point de vue, la valeur épistémique sémantique (Duval, 1995) de la conjecture est donc moins sûre que celle du postulat.