

Initier un processus de preuve mathématique dans un environnement de géométrie dynamique 3D
To Initiate a Mathematical Proof Process in an 3D Dynamic Geometry Environment
Revista Latinoamericana de Investigación en Matemática Educativa, vol. 17, supl. 4-2, 2014
Comité Latinoamericano de Matemática Educativa
Mithalal-Le Doze, J. (2014). Initier un processus de preuve mathématique dans un environnement de géométrie dynamique 3D. Revista Latinoamericana de Investigación en Matemática Educativa, 17 (4-2), 343-360. http://dx.doi.org/10.12802/relime.13.17417
Reçu: 28 Janvier 2013
Accepté: 29 Août 2013
Résumé: Cette contribution s’inscrit dans le thème : « Le travail mathématique et les aspects sociaux et institutionnels ». Nous avons ici souhaité interroger comment, dans le contexte d’une activité de construction géométrique, l’emploi de preuve intellectuelle peut se trouver justifié et de quelle manière il contribue à inscrire de manière stable l’activité des élèves dans une géométrie axiomatique naturelle. Dans notre travail de thèse nous avions montré que des situations construites dans un environnement de géométrie dynamique 3D pouvaient conduire les élèves à s’appuyer sur ce type de géométrie. En revanche, cette évolution s’avérait généralement instable, et nous proposons ici d’interroger en quoi les interactions sociales, et notamment via la genèse discursive, jouent un rôle fondamental quant à cette stabilité. La question de la preuve se trouve au cœur de cette problématique, puisqu’elle semble en réalité consubstantielle du passage d’une géométrie GI assumée à une géométrie GII morcelée. Nous proposons ici d’analyser le travail de trois groupes d’élèves, tiré d’une expérimentation de thèse (Mithalal, 2010), afin de mettre en lumière les interactions entre l’activité matérielle et la genèse discursive dans les espaces de travail géométrique.
Mots clés: Environnement de géométrie dynamique 3D, Genèse discursive, Preuve, Espaces de Travail Géométrique.
Resumen: Esta colaboración se inserta en el tema: «El trabajo matemático y los aspectos sociales e institucionales». Hemos querido examinar aquí cómo, en el contexto de una actividad de construcción geométrica, el empleo de una demostración intelectual puede encontrarse justificado y de qué manera éste contribuye a insertar de manera estable la actividad de los alumnos en una geometría axiomática natural. En nuestro trabajo de tesis habíamos mostrado que situaciones construidas en un ambiente de geometría dinámica 3D podían llevar a los alumnos a apoyarse en este tipo de geometría. En cambio, esta evolución mostraba ser generalmente inestable, y se propone aquí investigar en qué las interacciones sociales, y en especial vía la génesis discursiva, juegan un papel fundamental en lo que se refiere a esta estabilidad. La cuestión de la demostración se encuentra justo en el centro de esta problemática, ya que parece en verdad consubstancial del paso de una geometría GI asumida a una geometría GII fragmentada. Aquí proponemos analizar el trabajo de tres grupos de alumnos, inspirado en un experimento de tesis (Mithalal, 2010), con el fin de develar las interacciones entre la actividad material y la génesis discursiva en los espacios de trabajo geométrico.
Palabras clave: Ambiente de geometría dinámica 3D, Génesis discursiva, Demostración, Espacios de Trabajo Geométrico.
Abstract: This paper concerns the topic: “The mathematical work and the social and institutional aspects.” We have attempted to analyze how, in a geometrical construction activity context, the use of intellectual proof can be justified and which way it contributes to stably insert the students’ activity in a natural geometrical axiom. In our thesis project we have shown that situations built on a 3D dynamic geometrical environment can lead the students to rely on this type of geometry. Nonetheless, this evolution would proof itself unstable, and we propose here to examine where the social interactions, and especially via discursive genesis, play a fundamental role in terms of this stability. The proof issue is central to this concern, as it seems to be consubstantial with the transition of assumed Geometry GI to parceled Geometry GII. We propose to analyze the work of three groups of students, inspired on a thesis experiment (Mithalal, 2010), with the purpose of highlighting the interactions between the material activity and the discursive genesis in the geometrical working spaces.
Keywords: 3D dynamic geometrical environment, Discursive genesis, Proof, Geometrical Working Spaces.
Resumo: Esta colaboração se insere no tema: «O trabalho matemático e os aspectos sociais e institucionais». Quisemos examinar aqui como, no contexto de uma atividade de construção geométrica, o uso de uma demonstração intelectual pode ser justificada e de que maneira isso contribui na inserção, de maneira estável, da atividade dos alunos em uma geometria axiomática natural. Em nosso trabalho de tese, tínhamos mostrado que situações construídas em um ambiente geométrico dinâmico 3D podiam levar os alunos a se apoiarem neste tipo de geometria. Por outro lado, esta evolução mostrava ser geralmente instável, e por isso nos propomos aqui pesquisar como as interações sociais, e em especial através da gênese discursiva, possuem um papel fundamental no que se refere a essa estabilidade. A questão da demonstração se encontra bem no centro desta problemática, pois parece na verdade consubstancial a passagem de uma geometria GI assumida a uma geometria GII fragmentada. Aqui propomos analisar o trabalho de três grupos de alunos, inspirado em um experimento de tese (Mithalal, 2010), com a finalidade de mostrar as interações entre a atividade material e a gênese discursiva nos espaços de trabalho geométrico.
Palavras-chave: Ambiente geométrico dinâmico 3D, Gênese discursiva, Demonstração, Espaços de Trabalho Geométrico.
1. Introduction
L’apprentissage de la preuve constitue un des points délicats de l’enseignement secondaire en géométrie. Il est largement étudié, tant pour la preuve elle - même, pour les différentes formes qu’elle peut prendre, que pour les différentes fonctions qu’elle revêt et les contextes qui motivent son utilisation. Une question corollaire consiste à interroger les différents obstacles à l’emploi de preuves mathématiques dans l’activité géométrique des élèves. C’est le point de vue que nous avions adopté dans notre travail de thèse (Mithalal, 2010), où cette question initiale de la preuve s’était incarnée dans une interrogation relative à l’emploi d’une géométrie axiomatique naturelle (Houdement & Kuzniak, 2006) et la mobilisation de la visualisation non iconique (Duval, 2005) chez les élèves. Nous souhaitons ici interroger les rapports entre les résultats mis en évidence et l’apparition éventuelle de preuve mathématique.
2. Stabilité de l’usage d’une géométrie GII
2.1. Motiver une géométrie axiomatique naturelle
Nous faisons essentiellement référence aux travaux de Houdement et Kuzniak (2006) et à leur caractérisation de la géométrie naturelle (GI) et de la géométrie axiomatique naturelle (GII), aux travaux de Kuzniak (2010), ainsi qu’aux travaux de Duval (2005).
Kuzniak (2010) propose de situer l’activité géométrique dans deux plans, le plan épistémologique décrivant essentiellement le contexte épistémologique dans lequel va s’inscrire le travail géométrique du sujet, tandis que le plan cognitif s’attache plus spécifiquement à l’activité du sujet, aux moyens qu’il met en œuvre pour résoudre les problèmes de géométrie. Comme l’indique l’introduction du présent ouvrage, les plans sont en relation, et trois genèses – sémiotique, instrumentale, discursive – rendent compte des interactions. Pour autant, ces genèses sont en étroite relation et ne doivent en aucun cas être envisagées séparément ; aussi nous cherchons à montrer que dans certains cas l’évolution des ETG d’élèves est en réalité tributaire d’interactions permanentes, très fortes, entre genèse instrumentale et genèse discursive.
Les travaux de Duval (2005) sont à ce titre éclairant, car ils s’attachent fortement à l’activité du sujet, et notamment aux différentes manières d’appréhender les représentations et d’opérer sur celles-ci. En particulier, Duval distingue trois manières d’opérer sur les dessins 1 , dont deux nous intéressent ici : la déconstruction instrumentale et la déconstruction dimensionnelle.
La première consiste en l’assimilation d’un objet géométrique à un processus de construction par lequel il est obtenu : elle procède d’une étude analytique, mais est temporalisée et fortement dépendante des instruments utilisés. La seconde caractérise un objet par l’assemblage d’unités de dimensions inférieures (les unités figurales), la cohérence étant garantie par des propriétés géométriques explicitées. En sus de l’étude analytique, la description est cette fois détemporalisée et plus générique, et on voit ainsi que ces deux déconstructions font largement signe vers les genèses instrumentale et discursive.
Si la déconstruction instrumentale fait déjà largement signe vers l’objet géométrique par la décomposition qu’elle impose, Duval qualifie le second processus d’”essentiellement discursif”, l’envisage comme une condition nécessaire à la démonstration, et nous montrons qu’il est consubstantiel du paradigme GII. Nous avons montré (Mithalal, 2010) qu’il est possible de concevoir des situations de construction, dans un environnement de géométrie dynamique 3D, qui favorisent la mobilisation d’une géométrie de type GII par les élèves, en vue de l’interprétation et de la résolution des problèmes qui leur étaient posés, sans injonction explicite de la part de l’enseignant.
L’approche instrumentale (Rabardel, 1995) nous permet d’envisager a priori différents usages des artefacts mis à la disposition de l’élève, certains de ces usages étant exclusivement dirigés vers une action sur les objets matériels, d’autres s’appuyant en revanche sur des connaissances géométriques plus élaborées – et correspondant à l’instanciation dans un cadre graphique d’opérations réalisées sur la figure. Il est de fait possible de distinguer deux déconstructions instrumentales proches, la première permettant de répondre à des problèmes posés dans GI, la seconde s’inscrivant plus fortement dans GII tant pour l’interprétation des problèmes que pour les outils de résolution employés. Nous avons montré qu’un basculement de la première à la seconde forme de déconstruction s’opère lors d’un travail sur des situations adaptées. Dans ce cas, les connaissances géométriques de type GII trouvent une légitimité via les usages qu’elles permettent, ce qui contribue au fil du temps à inscrire l’activité géométrique de l’élève dans une géométrie axiomatique naturelle. C’est en fin de compte l’interprétation même des problèmes qui peut se trouver modifiée.
Ce passage entre les deux déconstructions témoigne d’une interaction forte entre les deux genèses, discursive et instrumentale, mais il importe de montrer qu’elle n’est ni simple, ni univoque, et qu’en particulier elle ne peut se résumer à considérer que la genèse instrumentale est simplement traduite dans la genèse discursive. Ceci est illustré de manière particulièrement frappante lorsqu’on interroge le caractère durable des évolutions suscitées.
2.2. Le problème de la stabilité
Dans les expérimentations mentionnées, les objets mathématiques semblent fréquemment cantonnés au rôle d’outils pour la résolution des problèmes, et n’interviennent pas naturellement pour leur interprétation – ceci pouvant être lié à la nature des activités mathématiques. Les élèves observés, en classe de seconde, considèrent souvent que le problème porte sur les objets matériels et ont essentiellement recours à des outils mathématiques élaborés de manière ponctuelle, pour pallier les déficiences d’un examen purement perceptif.
L’exemple suivant illustre en outre un phénomène fréquent de déplacement progressif de l’enjeu de l’activité vers l’objet géométrique. Ces élèves de seconde travaillent en trinôme à un problème de reconstruction d’une partie manquante d’un cube (voir figure ci-dessous), dans le logiciel de géométrie dynamique Cabri 3D. Initialement, l’attention est essentiellement portée sur la reconstruction d’un objet matériel, et l’activité est en fait ancrée dans GI. Ainsi l’échange suivant, renvoyant vers un problème de GI :
03’33, E1 : Aaaaaah, t’es trop fort ! Mais sauf qu’il faut que tu remplisses maintenant!
03’39, E2 : Monsieur ? Il faut le remplir le cube, ou juste le reconstruire ?
Peu à peu, les élèves sont confrontés à des indéterminations visuelles (13’24, E2 : Ben tu fais au hasard à ce moment là !) et sont conduits à s’appuyer ponctuellement sur des connaissances géométriques plus élaborées (20’58, E1 :Tu prends la symétrique de ce point, à cet axe, comme ça tu le trouves là. Avoue !) Finalement, au moment de juger de la différence entre deux procédures de construction, les élèves s’appuient sur la déconstruction dimensionnelle employée,et non plus sur la forme ou les opérations de constructions employées. (31’50, E2 :Attends attends, parce que je viens d’y penser : le cube ne sert absolument à rien. […] C’est juste que t’as rajouté un cube des deux côtés 2 .) C’est finalement la construction géométrique de l’objet – dans une géométrie de type GII – qui devient source de validation et les conduits à rejeter une solution reposant sur une construction géométrique déjà employée. Pourtant, après avoir aussi radicalement changé leur manière d’interpréter le problème, les dernières constructions se sont de nouveau appuyées sur une interprétation purement matérielle de la question qui était posée (placer perceptivement un point « au bon endroit »), et GII semble n’apparaître que de manière épisodique.
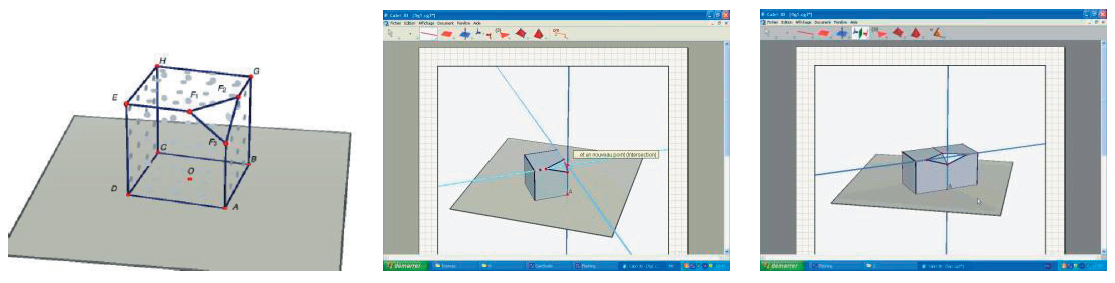
Ainsi, dans de nombreux cas, l’interprétation du problème varie effectivement, mais il semble que cela soit plus lié à un souci de cohérence entre les outils employés qu’à une réelle modification de la manière d’interpréter les problèmes de géométrie. Il en résulte une certaine instabilité quant au statut des problèmes de géométrie, les élèves s’appuyant indifféremment sur des interprétations que le chercheur qualifiera « de type GI » ou « de type GII ».
3. La question de la preuve en géométrie
3.1. Différent types de preuves
Au-delà des modalités de résolution des problèmes de géométrie ou de leur interprétation se pose la question de l’apprentissage de la démonstration, ou d’une manière plus générale des types de preuves employées par les élèves à des fins de validation. Balacheff (1999) distingue à ce propos explication, preuve, et démonstration (qu’il qualifie de « forme achevée de la preuve en mathématiques »). Nous nous appuyons ici sur les distinctions qu’il opère entre différents types de preuves :
Le calcul sur les énoncés dont fait mention Balacheff nous intéresse particulièrement dans la mesure où il se détache de l’action effective et se centre sur la construction logique d’énoncés, compatibles avec une géométrie de type GII. Nous cherchons ici à étudier comment le discours des élèves peut s’appuyer petit à petit sur ce type de calcul, et accorder une importance moindre aux preuves pragmatiques ou même à l’expérience mentale.
Cependant, dans un contexte d’activité de construction où la démonstration n’a pas de place réellement identifiée, nous choisissons de prêter une signification à certains objets du discours qui constituent des prémices à ce calcul : énoncé de règles valides permettant de fonder une argumentation, discussion quant à la validité de ces énoncés, schémas de preuve par contraposée, exhaustion, absurde…
3.2. Preuves intellectuelles dans une activité de construction
Le problème de la stabilité pose une question cruciale quant aux conditions qui peuvent motiver l’utilisation de preuves intellectuelles en vue de valider des constructions géométriques. Une hypothèse consistait à dire qu’en l’absence d’une possible validation perceptive ce type de preuve se trouverait nécessairement au centre de l’activité – et notamment des procédés argumentatifs – des élèves. Mais faute d’une modification stable de la manière dont ceux-ci abordent les problèmes de géométrie, le recours à des preuves pragmatiques (plus ou moins élaborées) peut demeurer parfaitement légitime aux yeux de certains élèves.
Pourtant, nous avons régulièrement pu observer des discours dont la teneur dépassait la seule expérimentation sur le dessin, tels qu’une interrogation portant sur des « théorèmes » jugés valides ou des raisonnements relativement élaborés. Nous cherchons ici à montrer que l’émergence de ces discours est consubstantielle de modifications significatives de l’ETM des élèves.
En particulier, il nous semble pertinent d’interroger le rôle de la genèse discursive : au-delà de la formulation qui a lieu – et donc des phénomènes qu’elle donne à voir au chercheur – elle motive la preuve à des fins d’argumentation. L’expérimentation menée alliait à la fois activité – éventuellement de construction – sur des objets matériels et interaction entre élèves, via le travail en binôme. Nous avons pu remarquer que le discours entre les élèves avait une incidence forte sur le statut des connaissances mathématiques employées, voire sur l’interprétation des problèmes de géométrie, comme nous le décrivons ci-dessous.
4. Etude de la coplanarité de deux droites
4.1. La situation
La situation proposée ici s’adresse à des élèves de seconde, et est la troisième séance de géométrie dans l’espace proposée dans notre ingénierie didactique. Elle fait suite à deux séances d’une heure, la première de découverte de l’environnement informatique, et la seconde de construction simple dont nous avons tiré l’exemple précédent.
Elle vise à faire construire la notion de non - coplanarité par des élèves qui n’ont pour référence, concernant les relations entre droites, que leurs connaissances de géométrie plane. Les indéterminations visuelles étant importantes, il est nécessaire d’établir des règles permettant une expérimentation sur les configurations de droites proposées pour décider de leurs relations. Une rapide justification sans contrainte formelle est demandée aux élèves. Notons qu’il s’agit d’élèves de seconde, qui ont donc des connaissances mathématiques élaborées et sont plus ou moins capables – sur demande – de mobiliser des connaissances théoriques et un schéma de démonstration. L’intérêt de cette situation réside plutôt dans l’observation de leur activité hors d’une injonction précise.
On donne aux élèves une série de 22 configurations (regroupées en trois groupes indiquées par leur numérotage) de deux droites construites dans Cabri 3D, et il leur est demandé de décider pour chacune d’entre elles siles droites se coupent. Nous reproduisons ci-dessous l’énoncé ainsi que quelques configurations.
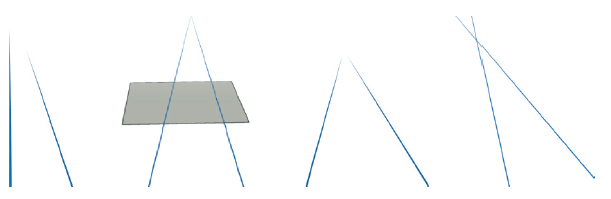
Enoncé : Vous trouverez [dans le dossier] des figures Cabri 3D préconstruite, numérotées de 1_1 à 3_7, qu’il va vous falloir étudier. Chaque fichier vous présente une configuration, avec deux droites construites. Vous devez déterminer, pour les deux premiers groupes de figures seulement, les cas où les droites proposées sont sécantes. Vous donnerez une brève justification de vos réponses sur cet énoncé.
La situation propose des objets simples et une consigne peu directive afin d’en permettre plusieurs lectures. En effet, la notion de droite peut renvoyerà différents objets (objets physiques matérialisés par le logiciel, objets physiques représentés dans le logiciel, objets géométriques représentés dans le logiciel),de même que le mot « sécantes » peut signifier qu’un point d’intersection est visible à l’écran, que les droites ne sont pas parallèles (comme en géométrie plane), qu’un point d’intersection existe mais n’est éventuellement pas représentéspar le logiciel, que le logiciel accepte de construire un point d’intersection, etc.
Il en résulte six interprétations possibles de l’activité 3 , plus ou moins ancrées dans une géométrie axiomatique naturelle, les trois premières ne considérant pas le problème de la coplanarité :
Les stratégies de résolution possibles sont relativement nombreuses, et nous pouvons en dégager quelques grandes catégories :
L’étude purement perceptive ou instrumentée des seuls objets matériels dans le logiciel Cabri 3D.
L’étude en référence à des connaissances de géométrie plane : les droites sont parallèles ou sécantes.
Le recours à l’outil informatique pour lever les cas d’indétermination (par exemple la construction d’un point d’intersection).
L’élaboration théorique de différents cas, comprenant la non-coplanarité, et conditionnant l’expérimentation sur les dessins.
Les configurations sont présentées de telle manière que chacune des lectures permette en apparence de résoudre un certain nombre de cas mais, si elle n’est pas assez élaborée, conduise à des indéterminations.
Enfin, la demande de justification vise essentiellement à provoquer une formulation par les élèves, tant pour offrir des observables qu’en faisant l’hypothèse d’un intérêt purement didactique à cette formulation, et sa qualité n’a pas vocation à être évaluée par l’enseignant.
Nous avons montré que cette situation conduisait de nombreux élèves à construire cette notion de non-coplanarité à partir de leur connaissance de géométrie plane. Selon les groupes et le type d’activité menée, cette notionprend différentes formes, depuis le très élaboré « voir si elles sont sur lemême plan » à « l’une au-dessous de l’autre », ou à la formulation de procédures instrumentées.
On voit aussi une gradation dans le degré de formulation, qui renvoie plus oumoins vers GII, et qui s’accompagne de discours argumentatif plus ou moins élaboré. La question est donc ici d’étudier les facteurs pouvant expliquer ce plus ou moins grand degré de formalisation, à travers trois cas prototypiques. Les deux premiers cas montrent que les modifications de l’ETM des élèves sont faibles lorsqu’une seule genèse est provoquée, celle-ci n’étant pas suffisante pour susciter les deux autres. Le dernier exemple, que nous développons davantage, illustre au contraire l’effet d’une synergie entre deux genèses, qui provoque une modification substantielle des différentes composantes de l’ETM.
4.2. Etude de cas : interactions entre les différentes genèses
Nous proposons ici d’illustrer par l’exemple de trois groupes que lorsque la situation ne suscite qu’une seule genèse, il s’ensuit une modification mineure de l’ETM. En revanche l’existence de deux genèses simultanées « provoque » la troisième, et l’importance des modifications est liée aux interactions permanentes de ces genèses. Les trois groupes présentés sont des élèves de seconde qui n’avaient suivi aucun cours de géométrie dans l’espace au coursde cette année, et pour qui la notion de coplanarité était totalement nouvelle.
Les interprétations proposées sont discutées dans Mithalal (2010), nous souhaitons avant tout ici mettre en avant une analyse en termes de genèses.
4.2.1. Premier groupe : recherche d’une interprétation théorique
Dans certains groupes, les connaissances de géométrie plane sont mises à mal, sans pour autant déboucher sur un discours argumentatif. En effet, la tâche est initialement interprétée à l’aide des connaissances de géométrie plane :
03’38, E2 : Ben je vois pas ce que tu veux dire, à part que «elles se coupent parce qu’elles sont pas parallèles»...
03’46, E1 : Ouais ben... Tu le mets? Elles sont pas perpendiculaires à un même truc, du coup.
Mais rapidement, les cas de non coplanarité remettent en cause cette interprétation, sans disposer d’une interprétation théorique fiable :
09’26, E2 : Genre si elles sont pas sur le même plan, elles ont beau ne pas être parallèles, elles ne se couperont pas
E1 : Quoi?
E2 : Si elles sont pas sur le même plan, même si elles sont pas parallèles, je crois qu’elles ne se coupent pas.
E1 : Ben pourquoi pas?
E2 : Ben je sais pas
E1 : Ben elles se couperont bien à un moment, quand elles sont parallèles elles...
Le discours des élèves va ici à contre - courant de l’impression visuelle, puisque les droits se coupent sur l’écran. Aussi, une genèse figurale n’a pas lieu d’être, dans la mesure où leur interprétation initiale concerne la figure. L’analogie avec des situations matérielles est de fait rapidement invoquée pour étudier les cas possibles, ce qui permet d’établir une règle qui sert ensuitede référence.
11’37, E2 : Non, mais regarde, par exemple t’es à la bastille, t’es au sommet de la bastille. Tu regardes le cours Jean Jaurès, eh ben tu le vois comme ça le cours Jean Jaurès alors que le cours Jean Jaurès il est... parallèle...
21’13, E1 : Ah oui d’accord elle va descendre et... Et comment on fait pour voir par rapport à la figure?
E2 : Oui donc c’est une histoire de plans en fait... […]
E2 : [l’enseignant est parti] Ah donc j’avais raison! Le truc des stylos, là...
E1 : Si il y en a une comme ça, une comme ça, ils sont pas sur le même plan!
E2 : Ça c’est un plan vertical, ça c’est un plan horizontal, et... oui ben j’avais raison! Bah maintenant on va le montrer.
Dans ce cas, les étudiants font montre d’une aisance avec un travail dans GII qui éclaire leur travail dans GI, en conséquence le consensus est rapidement trouvé et il ne leur est pas nécessaire de s’accorder. Des preuves empiriques ont été employées, non pas pour se convaincre mutuellement mais uniquement pour établir avec un degré de certitude raisonnable les outils nécessaires. En revanche, l’enjeu restant l’étude des configurations et non la convergence d’opinions, les preuves intellectuelles ne dépassent pas l’expérience mentale.
La genèse instrumentale qui conduit à trouver des méthodes pour identifier les cas de non-coplanarité est efficace et ne conduit pas à des incongruités manifestes qu’elle ne serait pas en mesure de résoudre. La genèse discursive n’est pas nécessaire, elle est de fait très faible, et l’embryon de réflexion théorique engagé ne fait pas appel à des preuves élaborées tout comme elle ne modifie pas radicalement le référentiel. Paradoxalement, la faible déstabilisation de leur ETM par la tâche rend le problème essentiellement instrumental, et cette seule genèse est insuffisante pour avoir un effet sur une éventuelle genèse discursive et susciter explicitement une démarche de preuve.
L’activité proposée peut n’être envisagée que comme une étude d’objets matériels. Dans ce cas, les rétroactions du milieu peuvent ne pas être en conflit avec l’expérience sensible des élèves. C’est par exemple le cas du groupe suivant, comme en témoigne leur première conversation.
4.2.2. Deuxième groupe : l’examen perceptif semble suffisant
L’activité proposée peut n’être envisagée que comme une étude d’objets matériels. Dans ce cas, les rétroactions du milieu peuvent ne pas être en conflit avec l’expérience sensible des élèves. C’est par exemple le cas du groupe suivant, comme en témoigne leur première conversation.
04’08, E2 : Ben oui elles sont sécantes.
E3 : Mais comment tu vois?
E4 : Parce qu’on voit qu’elles sont pas parallèles, et si elles sont pas parallèles c’est qu’elles sont sécantes.
E3 : Mais non, mais il faut justifier... Donc, alors, elles sont sécantes, oui... Pourquoi? Parce qu’on le voit. [rires]
E4 : Ben c’est simple, on....
L’interprétation des élèves est ancrée dans GI et, la validité se trouvant dans l’expérience sur le dessin, les preuves ne dépassent pas l’ostension (7’35, E3: Tu fais une distance de cette droite à cette droite... 0 centimètres! Ça veut dire qu’elles se coupent! Tu vois?) 4 tandis que les tentatives de convaincre ne reposent pas sur la rationalité du discours :
20’06, E3 : Mais t’as fait quoi, là?
E4 : Mais j’ai fait... Attends...
E3 : Mais remets sur le truc, là, parce que... Supprime tout!
E4 : Non, attends, je vais te remettre les droites d’une autre couleur, comme ça tu vas bien les voir...
22’01, E3 : Tu peux faire aussi avec un... Un triangle, je crois...
E4 : Je vais essayer de le faire avec des plans. Ouh là! Ben c’est la même que tout à l’heure, à peu près, là!?
E3 : Mais pourquoi tu veux faire un plan?
E4 : Bah pourquoi pas?
C’est donc aux qualités du milieu que nous pouvons en premier lieu attribuer l’absence de discours argumentatif : faute de rétroaction perceptible disqualifiant les preuves pragmatiques – ou encore la pertinence d’outils tirés de GI – les élèves n’ont pas de raison valable de faire appel à des preuves plus élaborées et leur activité reste limitée à l’action. Dans le cas présent, l’intégralité de la séance sera consacrée à ce type d’études.
Ici encore, la genèse instrumentale joue un rôle central et est la principale source de modification des ETM : pour savoir si deux droites se coupent, il vaut mieux mesurer la distance les séparant que regarder si elles sont parallèles. En revanche le référentiel figural n’est pas mis en défaut, et la genèse figurale n’a pas lieu d’être. De fait, aucun élément conflictuel ne se matérialise dans le discours, et la genèse discursive n’est pas engagée. Contrairement au groupe précédent, l’ETM n’est cette fois pas adapté au traitement de la tâche, ce qui se manifeste par des difficultés instrumentales, mais l’absence d’autre déstabilisation – et donc d’autre genèse – cantonne le problème à cette seule dimension instrumentale, ce qui ne donne pas lieu à une modification majeure de l’ETM.
4.2.3. Troisième groupe : conflit interprétatif
Les hypothèses relatives à l’intérêt de Cabri 3D (Mithalal, 2010) reposent en grande partie sur la non - univocité des informations visuelles perçues, les outils de GII permettant de concevoir des procédures rétablissant cette univocité. Dans le cas présent, il résulte de ce phénomène des divergences interprétatives entre les élèves du binôme qui ont deux conséquences. Premièrement, cela déplace l’enjeu de l’activité vers un examen rationnel, dans le discours, des interprétations possibles. En second lieu, cela conduit des élèves à établir des preuves – non formalisées – d’existence de différents cas pour assurer la validité des casuistiques que chacune propose.
Signalons que ce binôme est en réalité, en raison de contraintes matérielles, un trinôme. La troisième élève joue exclusivement le rôle de scribe, chargée de rédiger les conclusions et les brèves justifications. Cette position d’arbitre la conduit à mettre en scène la confrontation des deux autres élèves du binôme et à l’inscrire dans une activité discursive, détachée de l’examen direct d’une configuration particulière.
5. Interprétation initiale du problème et recherche de méthodes de résolution
Au cours des premières minutes, la référence porte essentiellement sur les caractéristiques spatiales des objets observés, qui sont situés dans l’espace sensible. Le mot « regarde » est omniprésent, et à défaut l’instrument sert d’arbitre. On voit assez rapidement apparaître une procédure perceptive instrumentée qui consiste à mettre les deux droites en surbrillance en même temps (ce qui permet d’affirmer qu’elles ont un point commun reconnu par le logiciel). Il faut aussi noter le mot « intersection » proposé par le logiciel, et qui intervient comme juge de paix.
La justification est ici inutile (3’30, E6 : Et puis il n’y a pas de justification, tu sais c’est... c’est la même!), dans la mesure où le logiciel rend l’examen sensiblesuffisant. Ici, seule une genèse instrumentale est à l’œuvre, qui ne débouche que surune modification mineure de l’ETM – les procédés instrumentaux jugés valides.
5.1. Traitement des indéterminations
Cependant, des cas d’ambiguïté apparaissent progressivement, et leur traitement évolue peu à peu. Ainsi à 10’44, à propos de la configuration reproduite ci-dessous:

E5 : Ah non regarde regarde regarde! Elles sont pas... elles sont pas... Elles se croisent pas, là, tu vois? Genre comme elles sont dans l’espace elles se touchent pas, en fait...
E6 : Ah ouais... Mais c’est un autre, ça?
E5 : Attends je vais voir un truc... Justement tu vois, on peut pas le... Tu vois? On peut même pas faire un point d’intersection, tu vois!
E6 : Comment je peux dire ça? Euh, droites dans l’espace...
À défaut d’une interprétation disponible, les explications sont très contextualisées et la référence à l’action perdure (12’08, E5 : De plus.... Tu mets: de plus, pas possible de faire un point d’intersection). C’est d’ailleurs cette procédure qui produit une règle pour l’étude des configurations suivantes :
12’13, E6 : Là je pense que c’est pareil...
E5 : Oui regarde regarde regarde regarde... Ah ça se voit trop bien là, regarde!
E6 : Ouais...
E5 : T’as vu? Faisons un point d’intersection, si possible... Pas possible... Donc...
E6 : Pareil. 3e... Pareil, exactement pareil qu’en 2.
Cette règle donne progressivement lieu à une nouvelle catégorie établie par analogie :
13’10, E5 : Ouais mais en fait non, elles sont... Elles se superposent, tu vois! Ouais... Tu mets «elles se superposent».
On voit ici que la conjonction de rétroaction négative du milieu perçue par les élèves – l’ambiguïté que nous avons mentionnée – et de tentative d’interprétationles conduit vers un questionnement plus décontextualisé et détaché de l’action. Pour autant, il ne s’agit pas encore d’une construction théorique achevée,celle-ci n’intervenant qu’ultérieurement.
Il faut tout de même noter que deux genèses sont identifiables immédiatement : une genèse instrumentale qui est le prolongement dela précédente, et une genèse figurale liée aux indéterminations visuelles. Laconjonction de ces deux genèses conduit les élèves à ne pas traiter leproblème que sous un seul de ses aspects, et donne de fait lieu à un débutde genèse discursive marquée par un discours qui n’est plus attaché à ununique cas. On ne trouve cependant dans ce discours ni preuve, ni modification duréférentiel théorique visible.
5.2. Élaboration théorique consécutive à des divergences d’interprétation
En effet, les interprétations des élèves divergent, notamment en raison de la polysémie des termes employés (19’47, E5 : Elles sont pas sur le même plan, elles sont dans l’espace!), ce qui conduit à des conclusions contradictoires dans certains cas, tel que le suivant :
18’19, E6 : Ben non puisque là c’est 89 degrés! Donc elles se coupent forcément quelque part!
E5 : Non! Non! Trop pas, parce que le prof il l’a dit tout à l’heure, il a ditque c’est pas forcément si elles sont perpendiculaire à une même droite qu’elles sont parallèles.
E6 : Mais elles sont pas parallèles, là.
E5 : Elles sont... Elles sont peut être pas parallèles, mais elles se touchent pas! Donc: elles se touchent pas!
C’est notamment ici que les référentiels théoriques de la géométrie plane sont explicitement invoqués et mis en doute, ce qui débouche sur la construction de nouvelles connaissances, et ainsi l’équivalence entre « parallélisme » et « perpendicularité à une même droite » est par exemple remise en cause :
18’52, E6 : Si, regarde, elles sont pas... elle est là, et l’autre elle est là! Je t’ai dit, c’est 89, les deux là elles sont parallèles, mais pas...
E5 : Oui ok, mais c’est pas pour ça qu’elles doivent se toucher, tu vois !
E6 : Oui parce qu’il en aura peut être une au dessus de l’autre.
E5 : Il n’y aura jamais un point d’intersection!
E6 : Parce qu’il y en a une au dessus de l’autre, mais c’est ça en fait ce que je voulais faire […]
19’30, E6 : Mais parce que, en fait il y a deux trucs c’est: soit, de toute façon à la base elles sont pas parallèles, donc si elles sont pas parallèles et qu’elles sont sur le même plan, eh bien elles se croisent.
C’est donc ici l’opposition d’interprétations qui conduit les élèvesde ce groupe à produire un discours plus générique, s’inscrivant dans une géométrie de type GII. Dans cette dernière phase, on voit simultanément lestrois genèses à l’œuvre, des considérations instrumentales et figurales intervenantdans la genèse discursive, et réciproquement. Des modifications fortes de l’ETM ont lieu, concernant à la fois le plan épistémologique (et l’évolution du référentiel) et le plan cognitif avec des visualisations et preuves différentes. Il apparaît que ce sont les synergies et les interactions entre ces trois genèses qui permettent ces modifications.
6. Conclusion
Dans cette étude de cas, il apparaît que les formes de preuves employées etleur rôle tiennent à la fois à l’enjeu identifié par les élèves – ce qu’il y a à prouver – et à l’interaction sociale qui motive cette preuve.
Bien entendu, la nature de l’activité géométrique exigée par la situation et la capacité du milieu à renvoyer des rétroactions perçues par les élèves estprimordiale, et faute de cette première condition on ne peut pas même raisonnablement espérer une modification de l’activité mathématique.
Pour autant, la qualité des rétroactions est visiblement insuffisante. En premier lieu car, à supposer que les élèves soient en mesure de dépasser leurs difficultés – ce qui n’est pas assuré –, les outils ne sont mobilisés que de manière ponctuelle, selon les besoins de l’exercice, et sont aussi rapidement abandonnés. Nous avons pu noter que lorsque l’enjeu est cantonné à l’action matérielle etque seule la genèse instrumentale a lieu, la stabilité de la modification de l’activité semble ne pouvoir être assurée. Les interactions sociales jouent donc un rôle prépondérant tant vis-à-vis de ce problème de stabilité que pour l’emploi de preuves intellectuelles. C’est par un conflit issu de l’action matériellemais actualisé dans le cadre de divergences inter-élèves qu’émerge undiscours argumentatif encré dans GII, et que l’activité géométrique est véritablement modifiée.
Soulignons encore, dans le dernier groupe observé, le rôle de la troisième élève, scribe, catalyseur de l’opposition entre les deux autres élèves, et garante de la qualité argumentative. Ce rôle ne doit pas être négligé et n’est passans faire penser – sans que les mêmes conditions soient à l’œuvre – au rôle organisateur de l’enseignant dans le débat scientifique (Legrand, 1993) (Bartolini Bussi, 1991), qui joue le rôle de catalyseur pour faire exister dans le discours des objets qui n’en sont pas initialement, et réciproquement, c’est-à-dire dans notre cas pour « propager » une genèse aux autres.
Plus généralement, ceci nous conduit à insister sur la double organisation, matérielle et sociale, nécessaire à l’émergence de preuve intellectuelle et à l’ancrage dans GII de manière stable – qui semblent en réalité consubstantiels.
Du point de vue des espaces de travail mathématique, cela illustre fortementla nécessité de ne pas penser les différentes genèses de manière disjointe,mais au contraire de les voir comme une synergie entre les trois types degenèses – chacune s’appuyant sur les autres. En définitive, et c’est dans ce sens que nous travaillons (Bulf, Mathé, & Mithalal, 2011), (Bulf C., Mathé, Mithalal, & Wozniak, 2012), cela nous conduirait à faire apparaître sur le schéma des genèses dans l’espace de travail géométrique (Kuzniak, 2010) la nécessitédes interactions entre les différentes genèses deux à deux.
Les références
Balacheff, N. (1999). Apprendre la preuve. Le concept de preuve à la lumière de l’intelligence artificielle, 197-236. (J. Sallantin, & J. J. Szczeciniarz, Éds.) Paris: PUF.
Bartolini Bussi, M. (1991). Social interaction and mathematical knowledge. Proceedings of the 15th PME International, (pp. 1-16). Assisi, Italia.
Bulf, C., Mathé, A. - C., & Mithalal, J. (2011). Language in geometrical classroom. Proceedingof the 7th Congress of the European Society for Research in Mathematics Education (CERME 7), (pp. 649-659). Rzeszow, Pologne.
Bulf, C., Mathé, A. - C., Mithalal, J., & Wozniak, F. (2012). Le langage en classe de Mathématiques : quels outils d’analyse en didactique des mathématiques? Questions vives en didactique des mathématiques : problèmes de la profession d’enseignant. Grenoble: La pensée sauvage.
Duval, R. (2005). Les conditions cognitives de l’apprentissage de la géométrie: développement de la visualisation, différenciation des raisonnements et coordination de leurs fonctionnements. Annales de Didactique et de Sciences Cognitves, 10, 5 - 53.
Houdement, C., & Kuzniak, A. (2006). Paradigmes géométriques et enseignement de la géométrie. Annales de Didactique et de Sciences Cognitives, 11, 175 - 193.
Kuzniak, A. (2010). Un essai sur la nature du travail géométrique en fin de la scolarité obligatoire en France. Proceedings of the First French - Cypriot Conference of Mathematics Education, (pp. 71 - 89).
Laborde, C. & Capponi, B. (1994). Cabri - géomètre constituant d’un milieu pour l’apprentissage de la notion de figure géométrique. Recherches en didactique des mathématiques 14 (1.2), 165-210.
Legrand, M. (1993). Débat scientifique en cours de mathématiques et spécificité de l’analyse. Repères IREM, 123-158.
Mithalal, J. (2010). Déconstruction instrumentale et déconstruction dimensionnelle dansle contexte de la géométrie dynamique tridimensionnelle. Grenoble: Thèse de l’Université de Grenoble.
Rabardel, P. (1995). Les hommes et les technologies. Approche cognitive des instruments contemporains. Paris: Armand Collin.
Notes
1 Nous distinguons ici dessin et figure au sens de Laborde et Capponi (1994).
2 Dans le cas présent, les élèves cherchaient une nouvelle méthode de construction, et si le processus de construction différait effectivement des précédents, la construction géométrique à laquelle il aboutissait était en revanche identique.
3 Pour une analyse a priori plus détaillée de cette situation, nous renvoyons à Mithalal (2010, pp. 156 - 171).
4 Rappelons qu’une distance « nulle » est tributaire de la précision de la mesure, aussi cette preuve n’est elle pas valide. D’autre part, dans un environnement de géométrie dynamique une telle propriété ne résiste pas nécessairement au déplacement, et rien dans la mesure ne garantit l’existence de la propriété géométrique d’intersection.